Equation defi

[GaBuZoMeu]

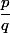
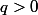
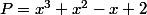
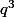
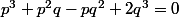
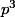
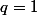
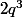
Je sors du cadre du lycée (quoique ...) pour parler de racines rationnelles et méthode de Horner. Si (avec et premiers entre eux et ) est une racine rationnelle de alors, en multipliant par pour chasser les dénominateurs, on obtient . Donc divise d'où puisque est premier avec et positif. Donc aussi divise d'où divise puisqu'il est premier avec . Les seules racines rationnelles possibles de sont . 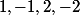On teste ces quatre possibilités par la méthode de Horner :



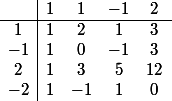
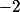
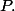
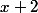
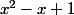
On lit dans le tableau que ; est donc la seule racine rationnelle de On lit aussi dans le tableau que le quotient de par est , dont on voit facilement qu'il n'a pas de racine réelle.

La méthode de Horner n'est pas très spectaculaire ici car le polynôme est tout petit et les candidats testés petits aussi. On peut voir la page wikipedia qui lui est consacrée.