Salut,
Lorsque tu encadre le "premier morceau", tu écrit que, pour tout
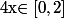
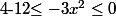
où le minimum (-12) est atteint pour x=2 et le maximum (0) est atteint pour x=0.
Lorsque tu encadre le "deuxième morceau", tu écrit que, pour tout
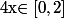
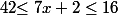
où le minimum (2) est atteint pour x=0 et le maximum (16) est atteint pour x=2.
Tu as évidement le droit de déduire de tes deux encadrement que, pour tout
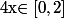
:
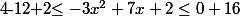
, sauf que le mini de cet encadrement
ne peut pas être atteint vu que, dans la première inégalité, pour avoir le mini., il faut prendre x=2 alors que dans la deuxième, il faut prendre x=0 et qu'on ne peut évidement pas prendre
à la fois x=0 et x=2 donc on ne peut pas avoir
à la fois -12 pour le "premier morceau" et 2 pour le "deuxième morceau".
A noter que, dans certains cas, l'inégalité obtenue avec cette méthode est "la bonne" (a condition que, dans les deux "petits" encadrements, les min et les max soient atteints pour les même valeurs de x). Par exemple, ça marcherais bien pour
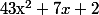
A bien noter aussi que l'encadrement obtenu par cette méthode est parfaitement valable, mais qu'il n'est pas "optimal".
