Détermination de la réciproque d une fonction
49 messages
- Page 2 sur 3 - 1, 2, 3
blocage au niveau de l exercice
salut capitaine nuggets
encore du blocage si possible de donner votre méthode avec des détailles
la fonction est définie sur ]-2,0[
elle est strictement décroissante sur ]-2,-1[ et elle est strictement décroissante sur]-1,0[
et on a f(-1)=0
donc la fonction réalise une bijection sur chaqu un des deux intervalles
comment déterminer les deux expressions de la réciproque ??
merci
encore du blocage si possible de donner votre méthode avec des détailles
la fonction est définie sur ]-2,0[
elle est strictement décroissante sur ]-2,-1[ et elle est strictement décroissante sur]-1,0[
et on a f(-1)=0
donc la fonction réalise une bijection sur chaqu un des deux intervalles
comment déterminer les deux expressions de la réciproque ??
merci
Salut,
A mon sens, ce n'est pas avec des limites que tu est sensé trouver la bijection réciproque (si la fonction n'était pas continue, ça ne marcherais pas). Tu doit le faire uniquement par du calcul.
Par exemple, pour la 2) (vu que la 1) est clairement fausse comme te l'a signalé capitaine nuggets.
Tu veut montrer que la fonction=\frac{x-1}{\sqrt{-x^2+2x}\) est une bijection de ]0,2[ sur
est une bijection de ]0,2[ sur 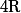 et déterminer sa bijection réciproque.
et déterminer sa bijection réciproque.
1) Perso, même si ce n'est pas demandé, je commencerais par vérifier que f est bien définie, c'est à dire qu'on peut calculer le truc en question pour n'importe quel x de ]0,2[ (on est jamais à l'abri d'une erreur d'énoncé...) :
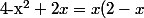>0\) pour
pour 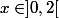 donc f est bien définie.
donc f est bien définie.
2) Ensuite, pour montrer qu'elle est bijective est déterminer sa bijection réciproque (on fait forcément les deux en même temps), on prend un y quelconque de l'ensemble d'arrivé, donc ici un 4$y\in{\mathbb R} et on cherche les éventuels x dans l'ensemble de départ tels que f(x)=y. Donc ici, le x qu'on cherche, il doit être dans ]0,2[ et, si f est effectivement bijective, alors il doit y avoir un et un seul x dans ]0,2[ qui vérifie f(x)=y (quelque soit le y pris au départ).
Au niveau calcul, on part donc de\) avec y réel connu et on cherche x dans ]0,2[.
avec y réel connu et on cherche x dans ]0,2[.
- Si y=0 alors clairement, la seule solution est x=0 qui est bien dans ]0,2[.
- Si y est non nul, alors (*) équivaut à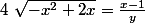 qui équivaut à
qui équivaut à ^2}{y^2}\) et
et  (à ne pas oublier :
(à ne pas oublier : \) )
)
^2}{y^2}\ \Leftrightarrow\ (y^2+1)x^2-2(y^2+1)x+1\) qui est une équation du second degré en x vu que y²+1 ne peut pas être nul.
qui est une équation du second degré en x vu que y²+1 ne peut pas être nul.
Le discriminant est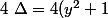^2-4(y^2+1)=4y^2(y^2+1)>0) donc l'équation admet deux solutions
donc l'équation admet deux solutions +2y\sqrt{y^2+1}}{2(y^2+1)} = 1+\frac{y}{\sqrt{y^2+1}}\) et
et 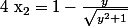 .
.
MAIS, il ne faut pas oublier les deux condition qu'on a sur le x cherché, à savoir que ce qui élimine la solution
ce qui élimine la solution 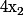 et que
et que 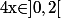 .
.
Il faut donc vérifier que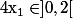 (je te laisse le faire, j'ai la flemme...) et on en déduira que f ext bijective de bijection réciproque
(je te laisse le faire, j'ai la flemme...) et on en déduira que f ext bijective de bijection réciproque 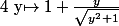 (formule valable y compris lorsque y=0)
(formule valable y compris lorsque y=0)
A mon sens, ce n'est pas avec des limites que tu est sensé trouver la bijection réciproque (si la fonction n'était pas continue, ça ne marcherais pas). Tu doit le faire uniquement par du calcul.
Par exemple, pour la 2) (vu que la 1) est clairement fausse comme te l'a signalé capitaine nuggets.
Tu veut montrer que la fonction
1) Perso, même si ce n'est pas demandé, je commencerais par vérifier que f est bien définie, c'est à dire qu'on peut calculer le truc en question pour n'importe quel x de ]0,2[ (on est jamais à l'abri d'une erreur d'énoncé...) :
2) Ensuite, pour montrer qu'elle est bijective est déterminer sa bijection réciproque (on fait forcément les deux en même temps), on prend un y quelconque de l'ensemble d'arrivé, donc ici un 4$y\in{\mathbb R} et on cherche les éventuels x dans l'ensemble de départ tels que f(x)=y. Donc ici, le x qu'on cherche, il doit être dans ]0,2[ et, si f est effectivement bijective, alors il doit y avoir un et un seul x dans ]0,2[ qui vérifie f(x)=y (quelque soit le y pris au départ).
Au niveau calcul, on part donc de
- Si y=0 alors clairement, la seule solution est x=0 qui est bien dans ]0,2[.
- Si y est non nul, alors (*) équivaut à
Le discriminant est
MAIS, il ne faut pas oublier les deux condition qu'on a sur le x cherché, à savoir que
Il faut donc vérifier que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
pour LaTeX voir :: http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.php
ensuite tes variations sont imprécises :
f est strictement croissante/décroissante de ....(intervalle) sur ....(intervalle ....)
ici il semblerait que f admette un minimum en -1 (d'après ton post (très) imprécis précédent) donc tu sais alors que y > 0 ... ce qui règle le pb des valeurs absolues ....
ensuite tes variations sont imprécises :
f est strictement croissante/décroissante de ....(intervalle) sur ....(intervalle ....)
ici il semblerait que f admette un minimum en -1 (d'après ton post (très) imprécis précédent) donc tu sais alors que y > 0 ... ce qui règle le pb des valeurs absolues ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
bon j'ai tracé la courbe avec geogebra ... et donc pour les variations il suffisait de dire que f est strictement croissante de ]0, 2[ dans R .... (on se fout du signe de y dans un premier temps)
puis éventuellement compléter par f(1) = 0 si nécessaire ensuite) ....
et entretemps Ben314 est intervenu et trouve comme moi ... en précisant la condition nécessaire .... que je n'avais pas donnée à 17h59 hier : à savoir que y et x - 1 ont même signe ....
puis éventuellement compléter par f(1) = 0 si nécessaire ensuite) ....
et entretemps Ben314 est intervenu et trouve comme moi ... en précisant la condition nécessaire .... que je n'avais pas donnée à 17h59 hier : à savoir que y et x - 1 ont même signe ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Ben314 a écrit:- Si y=0 alors clairement, la seule solution est x=1 qui est bien dans ]0,2[.
Une faute de frappe s'est glissée dans ton post Ben314 :+++:
En tout cas, c'est sympa pour lui de t'être décarcassé à faire tout le boulot :ptdr:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
pour déterminer les fonctions réciproques de f, on détermine
des intervalles I1 , I2 sur lesquels f est continue, strictement monotone.
Grace à la continuité de f, l'image d'un intervalle est un intervalle, ce qui assure la surjectivité
et la monotonie stricte assure l'injectivité.
Il existe donc des intervalles J1,J2 tels que la restriction de f à I1
induit une bijection de I1 sur J1.
Quand on calcule x=g(y) à partir de y=f(x), les choix à faire reflètent
les choix d'intervalles I1 ou I2
exemple y=cosh(x),x =Argcosh(y)
des intervalles I1 , I2 sur lesquels f est continue, strictement monotone.
Grace à la continuité de f, l'image d'un intervalle est un intervalle, ce qui assure la surjectivité
et la monotonie stricte assure l'injectivité.
Il existe donc des intervalles J1,J2 tels que la restriction de f à I1
induit une bijection de I1 sur J1.
Quand on calcule x=g(y) à partir de y=f(x), les choix à faire reflètent
les choix d'intervalles I1 ou I2
exemple y=cosh(x),x =Argcosh(y)
merci beaucoup pour votre soutien
salut Ben314
merci beaucoup c est très bien expliquer
mais pour le premier exemple je n est pas compris la faute
merci
merci beaucoup c est très bien expliquer
mais pour le premier exemple je n est pas compris la faute
merci
un exemple d application
salut mathelot
merci pour tes explications mais j aime bien savoir les appliquer sur un exemple avec les fonctions irrationnelles par exemple
est il possible de me donner une exemples d applications avec plus de détaille
pour que je puisse l appliquer
merci
merci pour tes explications mais j aime bien savoir les appliquer sur un exemple avec les fonctions irrationnelles par exemple
est il possible de me donner une exemples d applications avec plus de détaille
pour que je puisse l appliquer
merci
un autre exemple
salut
j ai essayé de chercher la fonction réciproque mais il y a un problème au niveau du choix des solutions
proposer moi une méthode
voici une fonction qui m a posé un problème
f(x)=1/3(x-2)^3 +1
f est continue et strictement croissante donc elle réalise une bijection de IR sur IR
déterminer sa fonction réciproque
merci bien
j ai essayé de chercher la fonction réciproque mais il y a un problème au niveau du choix des solutions
proposer moi une méthode
voici une fonction qui m a posé un problème
f(x)=1/3(x-2)^3 +1
f est continue et strictement croissante donc elle réalise une bijection de IR sur IR
déterminer sa fonction réciproque
merci bien
Hello, la forme sous laquelle tu as écrit ta fonction prête à confusion...
S'agit-il de=\frac{1}{3(x-2)^3}+1) ou
ou =\frac{1}{3(x-2)^3+1}) ou
ou =\frac{1}{3} (x-2)^3 +1) ???
???
S'agit-il de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Si tu poses ) , il suffit de résoudre l'équation d'inconnue d'inconnue
, il suffit de résoudre l'équation d'inconnue d'inconnue  et de paramètre
et de paramètre  :
: ^3 +1) . Montre alors en cherchant à isoler
. Montre alors en cherchant à isoler  que
que }+2) .
.
:+++:
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
georgets555 a écrit:salut mathelot
merci pour tes explications mais j aime bien savoir les appliquer sur un exemple avec les fonctions irrationnelles par exemple
est il possible de me donner une exemples d applications avec plus de détaille
pour que je puisse l appliquer
merci
énoncé
soit
1) étudier les variations de c et s.
2) calculer
Montrer que sinh() admet une réciproque h sur R tout entier
et cosh admet deux fonctions réciproques, l'une à valeurs dans R+, l'autre à valeurs
dans R-
comment passer a la racine cubique il y a un problème
salut capitaine nuggets
f est une bijection de IR sur IR
f(y)=x équivaut à (y-2)^3=3(x-1) comment passer a la racine cubique il y a un problème
merci
f est une bijection de IR sur IR
f(y)=x équivaut à (y-2)^3=3(x-1) comment passer a la racine cubique il y a un problème
merci
georgets555 a écrit:salut mathelot
Donc comment appliquer tes remarques svp
merci
ici
calcul de la fonction réciproque du cosinus hyperbolique.
calcul de
Choix des intervalles
[quote="mathelot"]
vous m avez pas compris c est comment choisir les intervalles J1 et J2 ? I1 , I2
voir l exemple suivant si possible de me donner une solution
f est une bijection de IR sur IR
f(y)=x équivaut à (y-2)^3=3(x-1) comment passer a la racine cubique il y a un problème
votre proposition
(pour déterminer les fonctions réciproques de f, on détermine
des intervalles I1 , I2 sur lesquels f est continue, strictement monotone.
Grace à la continuité de f, l'image d'un intervalle est un intervalle, ce qui assure la surjectivité
et la monotonie stricte assure l'injectivité.
Il existe donc des intervalles J1,J2 tels que la restriction de f à I1
induit une bijection de I1 sur J1.
Quand on calcule x=g(y) à partir de y=f(x), les choix à faire reflètent
les choix d'intervalles I1 ou I2)
merci
vous m avez pas compris c est comment choisir les intervalles J1 et J2 ? I1 , I2
voir l exemple suivant si possible de me donner une solution
f est une bijection de IR sur IR
f(y)=x équivaut à (y-2)^3=3(x-1) comment passer a la racine cubique il y a un problème
votre proposition
(pour déterminer les fonctions réciproques de f, on détermine
des intervalles I1 , I2 sur lesquels f est continue, strictement monotone.
Grace à la continuité de f, l'image d'un intervalle est un intervalle, ce qui assure la surjectivité
et la monotonie stricte assure l'injectivité.
Il existe donc des intervalles J1,J2 tels que la restriction de f à I1
induit une bijection de I1 sur J1.
Quand on calcule x=g(y) à partir de y=f(x), les choix à faire reflètent
les choix d'intervalles I1 ou I2)
merci
un problème au niveau de la justifications des passages et du choix de la solution
salut Ben314
cher professeur j ai un problème au niveau de la justifications des passages et du choix de la solution ou les solutions si possible de me donner une methode
voici un exemple
f est une bijection de IR sur IR
f(y)=x équivaut à (y-2)^3=3(x-1) comment passer a la racine cubique il y a un problème
merci
cher professeur j ai un problème au niveau de la justifications des passages et du choix de la solution ou les solutions si possible de me donner une methode
voici un exemple
f est une bijection de IR sur IR
f(y)=x équivaut à (y-2)^3=3(x-1) comment passer a la racine cubique il y a un problème
merci
comment faire sans utilisation de logiciels
salut zygomatique
merci pour ton message
j aime bien savoir comment faire sans utilisation de logiciels
les étapes a faire chaque fois
merci
merci pour ton message
j aime bien savoir comment faire sans utilisation de logiciels
les étapes a faire chaque fois
merci
49 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 109 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
