Dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
alizette
- Membre Naturel
- Messages: 44
- Enregistré le: 31 Mai 2007, 17:08
-
 par alizette » 13 Déc 2007, 15:13
par alizette » 13 Déc 2007, 15:13
bonjour a tous!
voilà j'ai un exercice a faire alors je connais la méthode pour trouver la tangente a ma courbe mais pour cela il me faut l'equation de la courbe parabole..mais je n'y arrive pas! je sais qu'elle est du type ax²+bx+c mais j'arrive pas a trouver les coefficients!
le but de lexercice étant de trouver la tangente a la courbe passant par E
voici le dessin

merci d'avance
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 13 Déc 2007, 15:18
par Quidam » 13 Déc 2007, 15:18
Si y=g(x) est l'équation de la parabole, il est clair que g(-1)=g(3)=0.
Par conséquent, g(x)=a(x+1)*(x-3)
En outre, g(1)=1, d'où 1=a*2*(-2) et a=-1/4.
g(x)=(-1/4)(x+1)*(x-3)

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 13 Déc 2007, 15:21
par raito123 » 13 Déc 2007, 15:21
Franchement je ne vois aucune courbe passante par E ce n'est pas b par hasars
Les multiples ne doivent pas être utilisés sans nécessité

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 13 Déc 2007, 15:23
par raito123 » 13 Déc 2007, 15:23
Quidam a écrit:Si y=g(x) est l'équation de la parabole, il est clair que g(-1)=g(3)=0.
Par conséquent, g(x)=a(x+1)*(x-3)
En outre, g(1)=1, d'où 1=a*2*(-2) et a=-1/4.
g(x)=(-1/4)(x+1)*(x-3)
Je crois qu'elle a dit une courbe passante par E et pas la fonction .
Les multiples ne doivent pas être utilisés sans nécessité
-
alizette
- Membre Naturel
- Messages: 44
- Enregistré le: 31 Mai 2007, 17:08
-
 par alizette » 13 Déc 2007, 15:29
par alizette » 13 Déc 2007, 15:29
excusez moi si je me suis mal exprimé il me semblait que c'était claire
Le but de de l'exercice est de trouver la tangente a la parabole passant par E (c'est la tangente qui passe par E non la courbe)
Pour que j'arrive a faire ça moi j'essaye de trouver l'equation de la parabole mais je n'y arrive pas!
merci d'avance

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 13 Déc 2007, 15:37
par raito123 » 13 Déc 2007, 15:37
Non ce ne'st pass cela car il y en a plusieurs parabole passante par E :
E peut être la valeur max comme peut-être la valeur min de la fonction
att je fais quelques démonstration sur mon papier
Les multiples ne doivent pas être utilisés sans nécessité
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 13 Déc 2007, 15:39
par Quidam » 13 Déc 2007, 15:39
raito123 a écrit:Je crois qu'elle a dit une courbe passante par E et pas la fonction .
alizette a écrit:le but de lexercice étant de trouver la tangente a la courbe passant par E
Je pense moi, qu'elle s'est simplement mal exprimée, c'est-à-dire exprimée de façon ambiguë.
Elle voulait dire : le but de l'exercice étant de trouver la tangente passant par E a la courbe !
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 13 Déc 2007, 15:41
par Quidam » 13 Déc 2007, 15:41
alizette a écrit:excusez moi si je me suis mal exprimé il me semblait que c'était claire
Le but de de l'exercice est de trouver la tangente a la parabole passant par E (c'est la tangente qui passe par E non la courbe)
Pour que j'arrive a faire ça moi j'essaye de trouver l'equation de la parabole mais je n'y arrive pas!
merci d'avance
J'avais bien compris ! Elle ne te plaît pas ma solution ?
http://www.maths-forum.com/showthread.php?p=317278#post317278

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 13 Déc 2007, 15:44
par raito123 » 13 Déc 2007, 15:44
Quidam a écrit:Si y=g(x) est l'équation de la parabole, il est clair que g(-1)=g(3)=0.
Par conséquent, g(x)=a(x+1)*(x-3)
En outre, g(1)=1, d'où 1=a*2*(-2) et a=-1/4.
g(x)=(-1/4)(x+1)*(x-3)
Je vois que tu tu cherchela réponse avec une fonction qui ne touchera jamais E
Les multiples ne doivent pas être utilisés sans nécessité

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 13 Déc 2007, 15:53
par raito123 » 13 Déc 2007, 15:53
Comme je t'ai dit plusieurs courbe passant par E peuvent avoir si on pose donc notre fon,ction tel que
=ax^2+bx+c)
on cherche donc la tangente en
)
donc
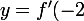(x+2)+f(-2))
avec
=4a-2b+c)
et
= \lim_{x\to-2} \frac{f(x)-f(-2)}{x+2})
en remplaçant f(x) et f(-2) et en simplifiant par
)
j'ai trouver que
=-2-2a+b)
et on se referant à
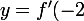(x+2)+f(2))
on obient: la l'equation de la tangente est
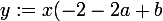+c-4)
Voilà c'est ma réponse je te pris que dés que tu as la coorection tu me renseigne!
Les multiples ne doivent pas être utilisés sans nécessité
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 13 Déc 2007, 15:54
par Quidam » 13 Déc 2007, 15:54
raito123 a écrit:Je vois que tu tu cherchela réponse avec une fonction qui ne touchera jamais E
Je ne cherche pas à toucher E ! Depuis tout à l'heure, tu t'obstines à ne pas comprendre ! Regarde ce qu'a écrit Alizette :
Alizette a écrit:
Le but de de l'exercice est de trouver la tangente a la parabole passant par E (c'est la tangente qui passe par E non la courbe)
Pour que j'arrive a faire ça moi j'essaye de trouver l'equation de la parabole mais je n'y arrive pas!
Elle ne cherche donc pas à faire passer une hypothétique parabole par E, mais elle cherche à trouver l'équation de la "tangente passant par E" à la parabole que l'on voit sur le dessin. Il est clair que cette parabole ne passe pas par E !

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 13 Déc 2007, 15:56
par raito123 » 13 Déc 2007, 15:56
En faite Quidam tu déja entendu parler d'une tangente qui qui a comme equation cartésienne qui ressemble à une parabole parce que le x² dit que ce que tu as trouver et faut?
Les multiples ne doivent pas être utilisés sans nécessité

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 13 Déc 2007, 15:57
par raito123 » 13 Déc 2007, 15:57
Quidam a écrit:Je ne cherche pas à toucher E ! Depuis tout à l'heure, tu t'obstines à ne pas comprendre ! Regarde ce qu'a écrit Alizette :
Elle ne cherche donc pas à faire passer une hypothétique parabole par E, mais elle cherche à trouver l'équation de la "tangente passant par E" à la parabole que l'on voit sur le dessin. Il est clair que cette parabole ne passe pas par E !
Je crois que je n'ai pas encore compris l'exo.
Les multiples ne doivent pas être utilisés sans nécessité
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 13 Déc 2007, 16:06
par Quidam » 13 Déc 2007, 16:06
raito123 a écrit:En faite Quidam tu déja entendu parler d'une tangente qui qui a comme equation cartésienne qui ressemble à une parabole parce que le x² dit que ce que tu as trouver et faut?
Alizette a bien précisé dès le départ : ce n'est pas l'équation de la tangente qu'elle veut ; elle saura la calculer dès qu'elle aura l'équation de la parable !
Ce qu'elle veut : c'est l'équation de la parabole ! alizette a écrit:voilà j'ai un exercice a faire alors je connais la méthode pour trouver la tangente a ma courbe mais pour cela il me faut l'equation de la courbe parabole..mais je n'y arrive pas! je sais qu'elle est du type ax²+bx+c mais j'arrive pas a trouver les coefficients!
Donc, je lui donne l'équation de la parabole ! Il va de soi, que ce n'est pas l'équation de la tangente (puisqu'elle sait la calculer seule !), mais bien l'équation de la parabole : la seule chose qu'elle a demandée !
Merci de te préoccuper de moi, mais
je n'ignore pas qu'une équation du second degré n'est pas l'équation d'une droite !

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 13 Déc 2007, 16:10
par raito123 » 13 Déc 2007, 16:10
okey merci et donc que diras-tu pour la deuxiéme partie
alizette a écrit:le but de lexercice étant de trouver la tangente a la courbe passant par E
voici le dessin
et aussi:
alizette a écrit:excusez moi si je me suis mal exprimé il me semblait que c'était claire
Le but de de l'exercice est de trouver la tangente a la parabole passant par E (c'est la tangente qui passe par E non la courbe)
Les multiples ne doivent pas être utilisés sans nécessité
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 13 Déc 2007, 16:30
par Quidam » 13 Déc 2007, 16:30
raito123 a écrit:okey merci et donc que diras-tu pour la deuxiéme partie
et aussi:
Certes, elle indique le but de l'exercice ! Mais elle a bien précisé auparavant qu'elle savait calculer une tangente dès l'instant qu'elle connaissait l'équation de la courbe et que c'était bien ce dernier point qui la dérangeait !

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 13 Déc 2007, 16:37
par raito123 » 13 Déc 2007, 16:37
Quidam a écrit:Certes, elle indique le but de l'exercice ! Mais elle a bien précisé auparavant qu'elle savait calculer une tangente dès l'instant qu'elle connaissait l'équation de la courbe et que c'était bien ce dernier point qui la dérangeait !
okey mais je me demande bien comment saura-elle calculer la tangente et elle n'a même pas la fonction dont la représentation passe par E?
Les multiples ne doivent pas être utilisés sans nécessité

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 13 Déc 2007, 16:48
par raito123 » 13 Déc 2007, 16:48
Au faite Quidam peut-tu revoir ce que j'ai fait dans le poste 10?
Les multiples ne doivent pas être utilisés sans nécessité
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 13 Déc 2007, 17:02
par Quidam » 13 Déc 2007, 17:02
raito123 a écrit:Au faite Quidam peut-tu revoir ce que j'ai fait dans le poste 10?
Ben, si tu veux :
Tu supposes qu'une parabole d'équation y=ax²+bx+c passe par E(-2;11/4) et tu cherches la tangente à la parabole en ce point.
raito123 a écrit: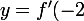(x+2)+f(-2))
avec
=4a-2b+c)
Je suis d'accord, mais on sait que f(-2)=11/4 !
raito123 a écrit:et
= \lim_{x\to-2} \frac{f(x)-f(-2)}{x+2})
en remplaçant f(x) et f(-2) et en simplifiant par
)
j'ai trouver que
=-2-2a+b)
C'est vrai que
= \lim_{x\to-2} \frac{f(x)-f(-2)}{x+2})
, mais on sait aussi que puisque f(x)=ax²+bx+c, f'(x)=2ax+b
Ici, je trouve f'(-2)=2*a*(-2)+b, soit f'(-2)=-4a+b
ce qui n'est pas la même chose que ce que tu as trouvé ! Je m'arrête ici, car ta suite ne peut être identique à la mienne !

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 13 Déc 2007, 17:08
par raito123 » 13 Déc 2007, 17:08
C'est vrai qu'on a trouver deux choses differentes mais la tienne est juste parce que moi j'ai oublié un a prés de -2 ce qui doit donner -2a et -2a-2a=-4a
donc si on continu on va avoir la même equation de la tangente
Je conclu que je dois faire une petite sieste mtn pour se réveiller en bonne forme et faire d'autres exo.
merci c'est gentil de ta part
Les multiples ne doivent pas être utilisés sans nécessité
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités

