Dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
melan0109
- Membre Relatif
- Messages: 350
- Enregistré le: 05 Jan 2008, 08:17
-
 par melan0109 » 17 Aoû 2010, 07:55
par melan0109 » 17 Aoû 2010, 07:55
Bonjour je voudrais savoir si la dérivée que je trouve est juste.
Soit f(x) = (x^3-2x²)/(x-1)²
Je trouve f'(x) = 2x^4-7x^3+x²-4x
Merci d'avance
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 17 Aoû 2010, 08:14
par Finrod » 17 Aoû 2010, 08:14
Je dirais que c'est faux (les coeff ne vont pas et il manque le dénomnateur)
Quant tu écris
=\frac{(3x^{2}-4x)(x-1)^{2}-2(x-1)(x^{3}-2x^{2})}{(x-1)^{4}})
penses a factoriser en haut par x(x-1), ça simplifie grandement les calculs.
-
melan0109
- Membre Relatif
- Messages: 350
- Enregistré le: 05 Jan 2008, 08:17
-
 par melan0109 » 17 Aoû 2010, 08:57
par melan0109 » 17 Aoû 2010, 08:57
je trouve donc
f'(x)= x(x-1)(2x²-5x+4)/(x-1)^4
-
melan0109
- Membre Relatif
- Messages: 350
- Enregistré le: 05 Jan 2008, 08:17
-
 par melan0109 » 17 Aoû 2010, 09:02
par melan0109 » 17 Aoû 2010, 09:02
Finrod a écrit:Je dirais que c'est faux (les coeff ne vont pas et il manque le dénomnateur)
Quant tu écris
=\frac{(3x^{2}-4x)(x-1)^{2}-2(x-1)(x^{3}-2x^{2})}{(x-1)^{4}})
penses a factoriser en haut par x(x-1), ça simplifie grandement les calculs.
Pourquoi on a un " -2 " avant le 2eme x-1 ?
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 17 Aoû 2010, 11:36
par Finrod » 17 Aoû 2010, 11:36
La dérivée de
^{2})
est
u'(x))
.
ça expliquerai pourquoi ce n'est pas encore le bon résultat.
Pour le +4 de 2x²-5x+4 par contre je suis d'accord.
-
Black Jack
 par Black Jack » 17 Aoû 2010, 12:39
par Black Jack » 17 Aoû 2010, 12:39
melan0109 a écrit:Pourquoi on a un " -2 " avant le 2eme x-1 ?
 = \frac{u(x)}{v(x)})
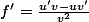
:zen:
-
melan0109
- Membre Relatif
- Messages: 350
- Enregistré le: 05 Jan 2008, 08:17
-
 par melan0109 » 17 Aoû 2010, 18:25
par melan0109 » 17 Aoû 2010, 18:25
Merci je viens de réagir.
A bientôt sur maths forum !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
