Dérivation

[Napapijri]

Bonjour

J'ai un fonction f(x)= (x au carré - 4x + 7) / (x au carré + 3)
Et on me demande de démontrer que f est bien définis sur R
Et je suis pas sûre de comprendre exactement...

Il faut faire f(x) = 0 ????
Ou
f(x) supérieur ou égal a 0 ???

...--"

[mathelot]

le dénominateur du quotient ne peut pas s'annuler.

[Napapijri]

le dénominateur du quotient ne peut pas s'annuler.

Et donc comme c'est formçement un nombre positif il est pas bien définis sur R ?
Mais enfaite R c'est bien tout les nombre : négatif ou positif et même décimaux ?

[Black Jack]

Et donc comme c'est formçement un nombre positif il est pas bien définis sur R ?
Mais enfaite R c'est bien tout les nombre : négatif ou positif et même décimaux ?

Je pense que tu n'as pas compris.

Il est interdit de diviser par 0.

Le dénominateur de f(x) (qui est x²+3) n'est jamais nul quelle que soit la valeur de x.

Donc f(x) existe quelle que soit la valeur de x dans R, on dit que f est définie sur R ... c'est à dire pour n'importe quelle valeur de x dans R.

Dit encore autrement, on peut calculer une valeur de f(x) quelle que soit la valeur de x choisie dans R.

Ce ne serait pas vrai, par exemple, si on avait : f(x)= (x² - 4x + 7) / (x² - 3)
en effet, pour x = Racinecarrée(3) (ou bien x = -racinecarrée(3)), on aurait x²-3 = 0
Comme il est interdit de diviser par 0, il est impossible de calculer la valeur de f(x) si x valait racinecarrée(3) (ou -racinecarrée(3))
Dans ce cas, f(x) ne serait pas définie sur R, mais seulement sur R duquel on aurait supprimé les valeurs -racinecarrée(3) et -racinecarrée(3).

On noterait alors que f est définie sur R/{-V3 ; V3}
(V est mis pour racine carrée)

:zen:

[Napapijri]

Je pense que tu n'as pas compris.

Il est interdit de diviser par 0.

Le dénominateur de f(x) (qui est x²+3) n'est jamais nul quelle que soit la valeur de x.

Donc f(x) existe quelle que soit la valeur de x dans R, on dit que f est définie sur R ... c'est à dire pour n'importe quelle valeur de x dans R.

Dit encore autrement, on peut calculer une valeur de f(x) quelle que soit la valeur de x choisie dans R.

Ce ne serait pas vrai, par exemple, si on avait : f(x)= (x² - 4x + 7) / (x² - 3)
en effet, pour x = Racinecarrée(3) (ou bien x = -racinecarrée(3)), on aurait x²-3 = 0
Comme il est interdit de diviser par 0, il est impossible de calculer la valeur de f(x) si x valait racinecarrée(3) (ou -racinecarrée(3))
Dans ce cas, f(x) ne serait pas définie sur R, mais seulement sur R duquel on aurait supprimé les valeurs -racinecarrée(3) et -racinecarrée(3).

On noterait alors que f est définie sur R/{-V3 ; V3}
(V est mis pour racine carrée)

:zen:

Oui d'accord j'ai compris
Merci bien

[Napapijri]

Oui d'accord j'ai compris
Merci bien

J'ai encore un problème ....
Après dans mon exercice on demande de cette déterminer la dérivé de f
J'ai trouvé (4x au carré - 8x - 12) / (x au carré + 3) au carré
Et ensuite on le demande d' étudier le signe de la dérivée
Alors pour le numérateur j'ai fait le discriminant x1 et x2 mais pour le dénominateur je coince ....

[capitaine nuggets]

Salut !

Un petit complément qui ne remplace pas ce qu'à pu dire Black Jack.
Quand on te demande de trouver sur quel sous-ensemble de , est définie, cela revient à déterminer pour quelles valeurs du réel , l'expression existe.

Les seules choses à savoir je dirais, c'est que :

1) la fonction "inverse"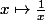 est définie sur ;
2) la fonction "racine carrée"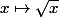 est définie sur .

Je dirai qu'à partir de ça, tu devrais pouvoir t'en tirer dans les exos :+++:

Tu pourras être amené à traiter des combinaisons comme par exemple :

Trouver sur quel sous-ensemble de , la fonction est bien définie.

[Black Jack]

J'ai encore un problème ....
Après dans mon exercice on demande de cette déterminer la dérivé de f
J'ai trouvé (4x au carré - 8x - 12) / (x au carré + 3) au carré
Et ensuite on le demande d' étudier le signe de la dérivée
Alors pour le numérateur j'ai fait le discriminant x1 et x2 mais pour le dénominateur je coince ....

(x²+3)² > 0 sur R

Et donc f'(x) a le signe de (4x² - 8x - 12)
... qui peut aussi s'écrire 4(x-3)(x+1)

Il suffit donc de faire un tableau de signes pour (x-3)(x+1) ... ce qui n'est pas insurmontable.

:zen:

[Napapijri]

J'avais réussi ;) je suis a l'exercice 2 maintenant ^^