Une limite de suite

[aviateur]

Bonjour
voici un exercice pas très standard (à mon avis) que je pose donc en énigme.
On considère la suite définie par


Déterminer le comportement à l'infini de (limite ou équivalent)

[pascal16]

comme il n'y a que cos² qui fait intervenir n et qu'il n'y a pas de singularité au dénominateur , on peut pas simplement remplacer le cos²(nx) par sa valeur moyenne ?

[aviateur]

comme il n'y a que cos² qui fait intervenir n et qu'il n'y a pas de singularité au dénominateur , on peut pas simplement remplacer le cos²(nx) par sa valeur moyenne ?

Bonjour
Je ne pense pas. en tout cas ça donne pas la bonne réponse.

[Lostounet]

Elle est marrante cette intégrale.
Elle me semble converger vers racine(2).

Si on lui soustrait l'intégrale de sin(x)/2 on se retrouve avec plein de petites bosses dont il faut quantifier l'aire: par exemple si n=5 on constate des pics symétriques centrés en x=pi/12 (par exemple).

À voir comment quantifier cela, on pourrait même penser à une transformée de Fourier pour se ramener à des fonctions triangle.

[aviateur]

Bonjour
Ok lostounet La réponse c'est racine(2). Pour une indication de solution je préfère ne rien dire. Il semblerait qu'il y a plusieurs façons alors il vaut mieux laisser développer les idées.

[Skullkid]

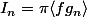
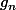
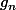
Bonjour, intuitivement l'idée de pascal16 doit marcher : en posant et , on a où les crochets désignent la moyenne sur [0,pi]. Comme oscille de plus en plus quand n grandit, on a envie de dire qu'à la limite, et deviennent "indépendantes", de sorte que .

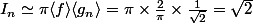
Plus formellement, (suite en blanc pour ceux qui veulent chercher) j'ai une démo qui consiste à couper l'intervalle d'intégration en n petits intervalles sur chacun desquels on peut encadrer le sinus du numérateur. On tombe au final sur un encadrement de I_n par deux sommes de Riemann qui ont la même limite. Ça se ramène à l'idée informelle ci-dessus en considérant que chaque petit intervalle correspond à une oscillation de g_n alors que f reste à peu près constante, mais il y a peut-être une démo qui exploite cette idée de manière plus explicite.

[aviateur]

Bonjour
@skullid cela semble possible qu'il y a une solution qui passe par là.
Alors il faut justifier que
1.
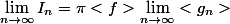
2. Montrer que

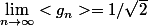
Bon après avoir réfléchi ça se démontre bien. ça fait 2 démos.

[aviateur]

Bonjour
Pour faire avancer un peu le problème je donne quelques indications:
Méthode 1 : (méthode qui n'utilise que des moyens élémentaires)
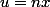
On fait d'abord le changement de variable et on se ramène à écrire sous la forme d'une somme d'intégrale de 0 à .....

Méthode 2: (méthode qui consiste à établir le résultat énoncé par @skullid)
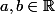
Montrer d'abord que pour tout la suite définie par
converge et déterminer sa limite.

Méthode 3 . (idée de @lostounet) Passer par les séries de Fourier. (ça marche aussi, j'ai fait les calculs).

[Lostounet]

[quote="aviateur"]