Suite bijective et limite!
Olympiades mathématiques, énigmes et défis
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Oct 2007, 13:08
par Nightmare » 29 Oct 2007, 13:08
Bonjour à tous :happy3:
Un petit défi pas simple du tout pour les fans d'analyse.
Soit
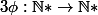
bijective et telle que la suite
}{n}\)_{n})
soit convergente.
Que vaut alors
}{n})
?
A vos claviers.
:happy3:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 29 Oct 2007, 17:23
par ThSQ » 29 Oct 2007, 17:23
On a envie de dire 1 :bad:
On tentative :
}{n}) Lemme bien
Lemme bien :
 \geq \frac{n(n+1)}{2})
Il suffit de constater que tous les
)
sont différents et sont donc au moins 1, 2, ..., n
Lemme aussi : si

est une bijection sur
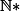
alors
 = \infty)
soit
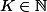
,
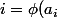)
, i = 1..K et donc
 \gt K)
si
)
1)
Si 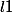
Alors pour n
 \leq (l+1)/2 \cdot n)
posons
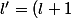/2 < 1)
 + ... + \phi(N_0-1) + \phi(N_0) + ... + \phi(n) \leq N_0(N_0+1)/2 + l'*(n*(n+1)/2 - l'*N_0(N_0+1)/2)
est incompatible avec le lemme bien pour n assez grand.
2)
si 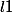
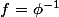
Alors d'après le lemme aussi
)/f(n) \rightarrow l)
soit
/n \rightarrow 1/l \lt 1)
et on est ramené au cas précédent :zen:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Oct 2007, 17:32
par Nightmare » 29 Oct 2007, 17:32
Joli :happy3:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 30 Oct 2007, 22:25
par aviateurpilot » 30 Oct 2007, 22:25
supposans que
}{n}\to l>1)
donc
>n)
donc
\subset [|1,N-1|])
donc
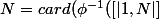)\le card(\subset [|1,N-1|])=N-1)
(absurde)
supposans que
}{n}\to l<1)
donc
<n)
donc
\subset [|1,N-1|])
donc
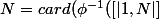)\le card(\subset [|1,N-1|])=N-1)
(absurde)
conclusion:
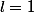
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 30 Oct 2007, 23:57
par ThSQ » 30 Oct 2007, 23:57
aviateurpilot a écrit:donc
>n)
donc
\subset [|1,N-1|])
Tu peux expliquer là ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 31 Oct 2007, 10:17
par yos » 31 Oct 2007, 10:17
ThSQ a écrit:Tu peux expliquer là ?
Les antécédents des entiers
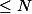
ne peuvent dépasser N-1 car à partir de N les images dépassent N.
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 01 Nov 2007, 01:37
par kazeriahm » 01 Nov 2007, 01:37
très joli aviateurpilot
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 01 Nov 2007, 11:29
par kazeriahm » 01 Nov 2007, 11:29
Dans le même genre mais déjà posté sur le forum,
si

est une injection de

dans

, que dire de la nature de la série
}{n^2+1})
?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 01 Nov 2007, 15:08
par ThSQ » 01 Nov 2007, 15:08
D'abord on remarque que
 \leq \sum_1^n 1/k)
Ensuite d'après Cauchy-Schwarz :
^2 = (\sum \frac{ \sqrt{b_i}}{a_i} \times \frac{1}{\sqrt{b_i}})^2 \leq \sum \frac{b_i}{a_i^2} \times \sum \frac{1}{b_i})
On applique ça avec
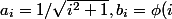)
et c'est fini.
ça diverge au moins en
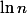
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 02 Nov 2007, 15:52
par aviateurpilot » 02 Nov 2007, 15:52
kazeriahm a écrit:Dans le même genre mais déjà posté sur le forum,
si

est une injection de

dans

, que dire de la nature de la série
}{n^2+1})
?
pour n fixé, on peux supposer que
,\phi(1),\phi(2),...,\phi(n)\}=\{a_0,a_1,a_2,...,a_n\})
tel que
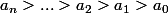
(donc
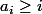
)
d'apres le reordonnement on a
}{k^2+1}\ge \bigsum_{k=0}^{n}\frac{a_k}{k^2+1}\ge \bigsum_{k=0}^{n}\frac{k}{k^2+1})
et on a
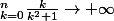
car
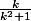
equivalente à
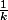
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités