Suite et limite (lycée)
Olympiades mathématiques, énigmes et défis
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 16 Juil 2006, 15:33
par Mikou » 16 Juil 2006, 15:33
LOl jai rien fait :p jai juste utilise la fonction sum de ma calculatrice ^^
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 16 Juil 2006, 15:46
par nekros » 16 Juil 2006, 15:46
:ptdr: :ptdr:
On pouvait remarquer que
(5^n-4^n)}=\frac{4^n}{5^n-4^n}-\frac{4^{n+1}}{5^{n+1}-4^{n+1}}})
On voit donc apparaître une somme télescopique...
Thomas G :zen:
-
calius
- Membre Naturel
- Messages: 39
- Enregistré le: 05 Juil 2006, 12:06
-
 par calius » 18 Juil 2006, 01:22
par calius » 18 Juil 2006, 01:22
salut
qu'est ce qu'une somme télescopique
desole je suis un aprenti :girl2:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Juil 2006, 01:24
par Nightmare » 18 Juil 2006, 01:24
Bonsoir :happy3:
C'est une forme de la forme
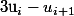
-
calius
- Membre Naturel
- Messages: 39
- Enregistré le: 05 Juil 2006, 12:06
-
 par calius » 18 Juil 2006, 01:26
par calius » 18 Juil 2006, 01:26
:ptdr: merci :ptdr:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Juil 2006, 01:29
par Nightmare » 18 Juil 2006, 01:29
Bien sûr je voulais dire "une somme de la forme" :marteau:
C'est la fatigue ... Je vais d'ailleurs me coucher, bonne nuit à tous ceux qui comme moi vont rejoindre le royaume des rêves.
:happy3:
-
calius
- Membre Naturel
- Messages: 39
- Enregistré le: 05 Juil 2006, 12:06
-
 par calius » 18 Juil 2006, 01:32
par calius » 18 Juil 2006, 01:32
bon nuit
moi encor je reste
@+ :++:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 18 Juil 2006, 01:34
par nekros » 18 Juil 2006, 01:34
salut,
Voici un exemple concret :
On prend
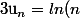-ln(n+1))
Imaginons que tu veuilles calculer
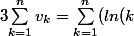-ln(k+1)))
On a donc
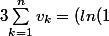-ln(2))+(ln(2)-ln(3))+(ln(3)-ln(4))+...+(ln(n)-ln(n+1)))
Tu vois donc que les termes s'éliminent :
Tu obtients donc
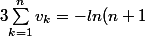)
Thomas G :zen:
-
calius
- Membre Naturel
- Messages: 39
- Enregistré le: 05 Juil 2006, 12:06
-
 par calius » 18 Juil 2006, 01:39
par calius » 18 Juil 2006, 01:39
j' utilise souvant c'ette methode mais helas je connais pas le nom
souvant pour les suites aritmetiques
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 18 Juil 2006, 01:40
par nekros » 18 Juil 2006, 01:40
ok, le principal c'est que tu saches t'en servir !
Thomas G :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
