Limite d'une suite

[chan79]

Bonjour
Soit la suite définie à partir de n=3 par
u(3)=cos( /3)
u(4)=cos( /3)*cos( /4)
u(5)=cos( /3)*cos( /4)*cos( /5)
...
u(n)=cos( /3)*cos( /4)*...*cos( /n)
soit
u(n)=u(n-1) * cos( /n)
j'aimerais bien savoir si cette suite visiblement convergente a comme limite 0 ou bien un autre nombre (lequel ?) :triste:

[Kikoo <3 Bieber]

Salut,

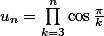Je fais sûrement erreur, mais et comme il s'agit d'un produit de termes finis (), la limite est 0 non ?

[Doraki]

log(un) = log(un-1) + log(cos(pi/n))
log(cos(x)) = -x²/2+O(x^4), donc pour n assez grand tu as log(cos(pi/n)) >= -pi²/2n², dont la somme converge. Donc la limite de ta suite est non nulle.

[chan79]

log(un) = log(un-1) + log(cos(pi/n))
log(cos(x)) = -x²/2+O(x^4), donc pour n assez grand tu as log(cos(pi/n)) >= -pi²/2n², dont la somme converge. Donc la limite de ta suite est non nulle.

Merci, je vais regarder ça :zen: