Limite d'une suite
Olympiades mathématiques, énigmes et défis
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 27 Sep 2008, 21:34
par acoustica » 27 Sep 2008, 21:34
Bonjour bonjour!
Petit exo pas facile je trouve:
Trouver la limite de
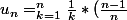^k)
en

.
voilavoila!
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Sep 2008, 21:48
par Zweig » 27 Sep 2008, 21:48
^{k}}{k}=\frac{1}{k})
donc la limite de ta fonction est
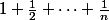
, sauf erreurs.
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 27 Sep 2008, 21:54
par acoustica » 27 Sep 2008, 21:54
pourquoi tu as retiré le message? c'était bon, non?
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 27 Sep 2008, 22:23
par acoustica » 27 Sep 2008, 22:23
Gloups, je comprends rien à cet article. :crash:
Est-tu sûr qu'il y a un rapport entre les deux?
leon1789 a écrit:je ne sais pas
oui, ça me fait ça aussi. :ptdr:
Autant la première question est faisable (même si carrément dure), autant la deuxième...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Sep 2008, 22:39
par leon1789 » 27 Sep 2008, 22:39
acoustica a écrit:Est-tu sûr qu'il y a un rapport entre les deux?
oui, on a
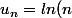- (\ \Phi(\frac{n-1}{n},1,n)-\frac{1}{n} \ )(\frac{n-1}{n})^n)
où

désigne la fonction phi de Lerch.
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 28 Sep 2008, 10:19
par acoustica » 28 Sep 2008, 10:19
leon1789 a écrit:oui, on a
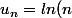- (\ \Phi(\frac{n-1}{n},1,n)-\frac{1}{n} \ )(\frac{n-1}{n})^n)
où

désigne la fonction phi de Lerch.
Mais de toute façon, le gars de licence moyen n'est sans doute pas censé connaître ça. Il y a forcement un autre moyen de procéder.
:look_up:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 28 Sep 2008, 13:15
par lapras » 28 Sep 2008, 13:15
salut,
je rappelle juste que les olympiades sont réservées aux lycéens et que ce genre d'exercices devrait être posté dans le supérieur.
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 28 Sep 2008, 14:02
par acoustica » 28 Sep 2008, 14:02
lapras a écrit:salut,
je rappelle juste que les olympiades sont réservées aux lycéens et que ce genre d'exercices devrait être posté dans le supérieur.
Oui, c'est vrai. A l'origine, je l'ai posté juste pour la première question, qui
elle est faisable par des lycéens.
J'ai juste rajouté après la deuxième pour ceux que ça interesse.
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 28 Sep 2008, 14:21
par acoustica » 28 Sep 2008, 14:21
Allez, j'ai retiré la deuxième. Là, c'est du 100% Olympiades!
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 28 Sep 2008, 21:00
par miikou » 28 Sep 2008, 21:00
slt, c'est quoi la seconde question?
Un= ln(n)+ L + o(1) c'est ca ?
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 29 Sep 2008, 09:01
par miikou » 29 Sep 2008, 09:01
on a facilement Un-> +infini
Un= ln(n) +( gamma +1)+ o(1) avec gamma la constante d'Euler ?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 30 Sep 2008, 09:18
par fatal_error » 30 Sep 2008, 09:18
Salut,
pour la première
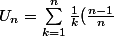^k)
Je poserais bien
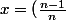)
D'où
=\sum_{k=1}^n \frac{x^k}{k})
et
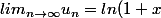=lim(ln(1-1/n+1))=ln(2))
edit:c'est pas ln (1+x), mais -ln(1-x)
On a donc
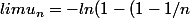)=-ln(1/n)=+\infty)
la vie est une fête


-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 30 Sep 2008, 11:03
par fatal_error » 30 Sep 2008, 11:03
Ah, je viens de voir que ce que j'ai fait, c'est faux. vu que je trouve une limite .
Par contre, je vois pas où. :-(
la vie est une fête

-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 30 Sep 2008, 19:00
par lapras » 30 Sep 2008, 19:00
Je crois que c'est un factorielle k et non k au dénominateur ;)

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 30 Sep 2008, 19:08
par fatal_error » 30 Sep 2008, 19:08
si c'est un factoriel k, on peut dans la même optique reconnaitre exp(x)-1 (vu qu'on commence a k=1 et non 0) d'ou
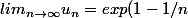-1=e-1)
enfin, je pense
la vie est une fête

-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 01 Oct 2008, 06:58
par miikou » 01 Oct 2008, 06:58
un diverge vers +inf semblerait -il

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 01 Oct 2008, 08:18
par leon1789 » 01 Oct 2008, 08:18
fatal_error a écrit:Salut,
pour la première
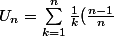^k)
Je poserais bien
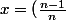)
D'où
=\sum_{k=1}^n \frac{x^k}{k})
et
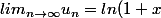=lim(ln(1-1/n+1))=ln(2))
edit:c'est pas ln (1+x), mais -ln(1-x)
On a donc
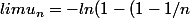)=-ln(1/n)=+\infty)
fatal_error a écrit:Ah, je viens de voir que ce que j'ai fait, c'est faux. vu que je trouve une limite .
Par contre, je vois pas où.

Mis à part une éventuelle erreur de calcul, il y a une énorme faute de raisonnement !
Tu poses
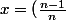)
, donc x dépend de n. ok.
Ensuite, tu passes à la limite
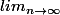
, mais comme par hasard, là x est constant... :marteau: c'est pas beau d'écrire des choses comme ça :
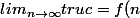)
!!!

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 01 Oct 2008, 08:20
par leon1789 » 01 Oct 2008, 08:20
miikou a écrit:slt, c'est quoi la seconde question?
Un= ln(n)+ L + o(1) c'est ca ?
oui, c'était ça.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 01 Oct 2008, 13:51
par lapras » 01 Oct 2008, 13:51
Pour la réponse, c'est +infini ;) (série harmonique tend vers +infini)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités