Suite et limite (lycée)

par **nekros** » 16 Juil 2006, 00:55

Salut,

Pour finir la soirée, ou commencer la matinée...

On définit pour tout

la suite

par la relation suivante :

Montrer que la série de terme générale

converge.
Déterminer la limite de

.

Bonne chance

Thomas G :zen:

par **Sdec25** » 16 Juil 2006, 01:15

Salut
euh, cette suite diverge, non ?

par **calius** » 16 Juil 2006, 01:26

je vois que ça converge plutot a 1
donc il sufit de monter que Un-1 ----> 0

par **nekros** » 16 Juil 2006, 09:22

salut,

La question est de trouver la limite de

Thomas G :zen:

par **Hilbert67** » 16 Juil 2006, 09:49

Tu es sûr de ton énoncé ? Parce qu'il me semble que même

tend vers l'infini ?!

par **nekros** » 16 Juil 2006, 09:59

Toutes mes excuses, je n'aurai pas du poster si tard... :dodo:

Thomas G :zen:

par **Sdec25** » 16 Juil 2006, 12:27

Pour la convergence de la suite et de la série :
En factorisant (ou directement) on peut trouver un équivalent :

C'est une série à termes positifs, la suite équivaut en

à une suite géométrique de raison 4/5 <1 donc la série converge.

par **nekros** » 16 Juil 2006, 12:38

Oui, sauf que c'est plutôt équivalent à

Tu as juste oublier un facteur :happy2:
Reste à trouver la limite...

Thomas G :zen:

par **Sdec25** » 16 Juil 2006, 12:42

arf je sais plus compter :ptdr:
je vais chercher la limite de la série maintenant.

par **nekros** » 16 Juil 2006, 13:42

Un indice ? :id:

Thomas G :zen:

par **Sdec25** » 16 Juil 2006, 14:01

Je veux bien :we:

par **aviateurpilot** » 16 Juil 2006, 14:05

tend vers 0

par **aviateurpilot** » 16 Juil 2006, 14:08

tend vers 0
car

tend vers -7
et

tens vers

par **Mikou** » 16 Juil 2006, 14:10

Oui, de plus la limite de le somme des uk tend vers L avec L < 125/81

par **nekros** » 16 Juil 2006, 14:15

L'indice : exprimer ce quotient sous la forme d'une différence de deux quotients.

Aviateurpilot, c'est la limite de

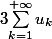
que l'on cherche et non celle de

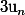
Thomas G :zen:

par **aviateurpilot** » 16 Juil 2006, 14:30

nekros a écrit:Aviateurpilot, c'est la limite .......

ok

nekros a écrit:L'indice : exprimer ce quotient sous la forme d'une différence de deux quotients.

j'aime pas les indice.
tu peus envoyer ce indice par un message privé.
en plus c'est ce que je voulais faire
je voulais exprimé cette somme en fonction de n
ou sous forme de au moin 2 sommes de deux suit plus simple en exprime

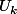
en fonction de

(*)
et ton indice est un cas particulire de ce que je voualis faire
:++:

par **nekros** » 16 Juil 2006, 14:39

ok désolé.
Mais avant de poster l'indice j'ai demandé si certains étaient intéressés...

Thomas G :zen:

par **aviateurpilot** » 16 Juil 2006, 14:45

c'et pour cela que je t'ai dit:

tu peus envoyer ce indice par un message privé.

par **Mikou** » 16 Juil 2006, 14:59

Manifestement la limite vaut 4, jai cherché deux suites geomtriques, l'une superieure a Un lautre inferieure a Un tel que la somme de leurs termes tend vers 4.
jai demontré que la premiere n'existe pas ... dommage

par **nekros** » 16 Juil 2006, 15:12

:++: Correct Mikou !

Thomas G :zen:

Suite et limite (lycée)

suite et limite (lycée)

Qui est en ligne