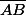Défi Lycée 13 - Problème d'optimisation
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 01 Aoû 2008, 21:28
par Zweig » 01 Aoû 2008, 21:28
Trouver le(s) point(s)

dans le plan d'un triangle ABC non obtusangle tels que la somme
 = m\cdot AP + n\cdot BP + p\cdot CP)
soit minimale, avec

,

et

des entiers naturels donnés.
Bonne chance !
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 01 Aoû 2008, 22:03
par _-Gaara-_ » 01 Aoû 2008, 22:03
Salut,
non obtusangle = acutangle ^^ pour précision :zen:
-
Fanatic
- Membre Relatif
- Messages: 270
- Enregistré le: 18 Juil 2008, 00:08
-
 par Fanatic » 02 Aoû 2008, 00:45
par Fanatic » 02 Aoû 2008, 00:45
Je comprends rien à cet énoncé. C'est quoi

? Ce sont des vecteurs ou quoi
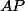
... ? C'est quoi la question ?
Un énoncé correct et bien formaté s'il te plait.
Zweig a écrit:Trouver le(s) point(s)

dans le plan d'un triangle ABC non obtusangle tels que la somme

soit minimale, avec

,

et

des entiers naturels donnés.
Bonne chance !
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 02 Aoû 2008, 10:36
par Zweig » 02 Aoû 2008, 10:36
Fanatic a écrit:Je comprends rien à cet énoncé. C'est quoi

? Ce sont des vecteurs ou quoi
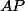
... ? C'est quoi la question ?
Un énoncé correct et bien formaté s'il te plait.
Voir le message de Rain' ... Je ne vois pas ce qu'il y'a d'ambigüe ! Si c'étaient des vecteurs, j'aurais mis une flèche ... t(P) est une distance dépendant de P uniquement (les entiers sont fixés).
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 02 Aoû 2008, 12:18
par Clembou » 02 Aoû 2008, 12:18
Zweig a écrit:Voir le message de Rain' ... Je ne vois pas ce qu'il y'a d'ambigüe ! Si c'étaient des vecteurs, j'aurais mis une flèche ... t(P) est une distance dépendant de P uniquement (les entiers sont fixés).
Moi aussi, j'ai mal compris l'énoncé car en géométrie, on note la longueur ou la distance entre deux points

et

:
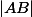
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 02 Aoû 2008, 12:23
par Flodelarab » 02 Aoû 2008, 12:23
Clembou a écrit:on note la longueur ou la distance entre deux points

et

:
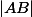
La réforme de la géométrie par Clembou.
Tout petit on apprend que la distance s'écrit AB.
Au pire tu as la distance algébrique
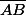
Ou encore la norme du vecteur
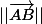
Mais utiliser la valeur absolue comme indicateur de distance, c'est la première fois que je vois ça.
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 02 Aoû 2008, 12:24
par Clembou » 02 Aoû 2008, 12:24
Flodelarab a écrit:La réforme de la géométrie par Clembou.
Tout petit on apprend que la distance s'écrit AB.
Au pire tu as la distance algébrique
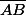
Mais utiliser la valeur absolue comme indicateur de distance, c'est la première fois que je vois ça.
Oui, voilà, Flo ! C'est bien cette notation qu'on attendait pour la distance algébrique. J'ai confondu avec une valeur absolue.
Merci de tes précisions :++:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 02 Aoû 2008, 12:51
par Zweig » 02 Aoû 2008, 12:51
Sauf que bon, ici la distance algébrique n'a aucun intêret !
Si tu veux, d'une manière plus rigoureuse :
 \rightarrow \mathbb{R})
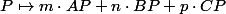
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 02 Aoû 2008, 14:06
par _-Gaara-_ » 02 Aoû 2008, 14:06
Ton exercice est difficile Zweig. C'est le top là.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 02 Aoû 2008, 14:11
par Zweig » 02 Aoû 2008, 14:11
Je n'ai jamais dit qu'il était facile :we:
Vous pouvez toujours me demander des indices !
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 02 Aoû 2008, 14:28
par _-Gaara-_ » 02 Aoû 2008, 14:28
Je t'avais demandé hier sur msn s'il fallait faire la disjonction de cas ?
Oui ou non ? XD
je pinaille grave
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 02 Aoû 2008, 14:30
par Flodelarab » 02 Aoû 2008, 14:30
Un indice: Ne cherchez pas P en dehors du triangle.
[Edit]Sauf si m n et p sont nul évidemment.[/Edit]
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 02 Aoû 2008, 14:32
par Zweig » 02 Aoû 2008, 14:32
Flodelarab > C'est marqué dans l'énoncé que P est dans le plan du triangle
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 02 Aoû 2008, 14:33
par Flodelarab » 02 Aoû 2008, 14:33
Et alors ? "Dans le plan" et "dans le triangle" sont synonymes ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 02 Aoû 2008, 14:36
par Zweig » 02 Aoû 2008, 14:36
Bah pour moi ça l'était, jusqu'à présent ... De toute façon, c'est assez "intuitif" que P est dans le triangle car bon, généralement dans les problèmes d'optimisation avec des triangles, les solutions sont des points remarquables de celui-ci.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 02 Aoû 2008, 14:52
par Flodelarab » 02 Aoû 2008, 14:52
T'as dérivé par rapport à quoi ?
Moi j'ai dérivé par rapport au temps et je trouve zéro.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 02 Aoû 2008, 15:25
par Imod » 02 Aoû 2008, 15:25
Ce problème est un grand "classique" : "Weighted Fermat triangle problem" . La solution s'appelle le point de Fermat ( curieux non ? ) . Je ne sais pas s'il y a une solution élémentaire mais il y a pas mal de littérature sur la question on the web !
Imod
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 02 Aoû 2008, 15:29
par Zweig » 02 Aoû 2008, 15:29
Hum, pas tout à fait Imod. Enfin, le problème de Steiner-Fermat-Toricelli c'est lorsque
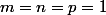
. Ici ce serait plutôt une généralisation.
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 02 Aoû 2008, 15:30
par _-Gaara-_ » 02 Aoû 2008, 15:30
Après quelques recherches je trouve que ce problème porte le nom de Fermat-Torricelli !
le mec il a mis longtemps avant de trouver..
Grillé..
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 02 Aoû 2008, 15:31
par Zweig » 02 Aoû 2008, 15:31
Mais bon, je ne voulais pas balancer le nom du problème sinon beaucoup aurait été tenté de faire des recherches et pour les moins sérieux, de balancer la solution trouvée. C'est d'ailleurs pourquoi j'ai donné la généralisation de ce problème, beaucoup plus difficile à trouver sur le Net ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
 dans le plan d'un triangle ABC non obtusangle tels que la somme
dans le plan d'un triangle ABC non obtusangle tels que la somme  = m\cdot AP + n\cdot BP + p\cdot CP) soit minimale, avec
soit minimale, avec  ,
,  et
et  des entiers naturels donnés.
des entiers naturels donnés. ? Ce sont des vecteurs ou quoi
? Ce sont des vecteurs ou quoi 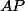 ... ? C'est quoi la question ?
... ? C'est quoi la question ? ? Ce sont des vecteurs ou quoi
? Ce sont des vecteurs ou quoi dans le plan d'un triangle ABC non obtusangle tels que la somme
soit minimale, avec
,
et
des entiers naturels donnés.
? Ce sont des vecteurs ou quoi
... ? C'est quoi la question ?
et
: