Somme des inverses des nombres premiers
Olympiades mathématiques, énigmes et défis
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 07 Déc 2008, 10:16
par lapras » 07 Déc 2008, 10:16
Bonjour,
Montrer que la somme des inverses des nombres premiers diverge.
Lapras
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 07 Déc 2008, 10:43
par nodgim » 07 Déc 2008, 10:43
Il me semble que cette question a été posée, je ne sais plus où. ça évolue comme le log du log, non?
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 07 Déc 2008, 10:46
par lapras » 07 Déc 2008, 10:46
Peut être, je ne sais pas...
:)
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 07 Déc 2008, 10:56
par ThSQ » 07 Déc 2008, 10:56
Si c'est classique (démo de Euler) et ça diverge en ln(ln(n)) donc faut pas être trop pressé non plus !
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 07 Déc 2008, 11:06
par lapras » 07 Déc 2008, 11:06
Je ne vous demande pas de ressortir la démo d'Euler ou Erdos. Je poste cet exo car il est, malgré les apparences, faisable de manière élémentaire. (quelques lignes).
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 07 Déc 2008, 11:22
par ThSQ » 07 Déc 2008, 11:22
Sauf erreur on t'a rien ressorti du tout, qu'est-ce tu racontes ?
Bien sûr c'est élémentaire quand on connait l'astuce. Quelqu'un qui la trouve vraiment tout seul ....
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 07 Déc 2008, 11:23
par ffpower » 07 Déc 2008, 11:23
une demo plus élémentaire que la formule d euler?je veux voir ca..
-
Redbul.
- Membre Naturel
- Messages: 22
- Enregistré le: 06 Mai 2008, 17:46
-
 par Redbul. » 07 Déc 2008, 11:28
par Redbul. » 07 Déc 2008, 11:28
comment fait on pour effacer un message ...
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 07 Déc 2008, 11:37
par lapras » 07 Déc 2008, 11:37
En fait dans cette démo il n'y a pas besoin de logarithmes ni rien. Je n'ai pas dit que c'était facile de trouver l'astuce !
Bonne chance :)
PS : l'astuce n'est pas de moi
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 07 Déc 2008, 11:46
par Imod » 07 Déc 2008, 11:46
D'un autre côté si la démo est plus astucieuse et plus courte que celle d'Euler ou d'Erdös , je vois mal le forumeur moyen la découvrir seul :doh:
Imod
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 07 Déc 2008, 11:46
par Zweig » 07 Déc 2008, 11:46
Du bouquin d'Hardy :
On suppose que la série est convergente. Alors on peut choisir un j tel que le reste de la série après le j-ème terme est plus petit que 1/2, ie :

. Donc
)
, le nombre d'entiers
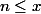
divisibles par au moins un des nombres
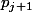
,
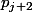
,... est inférieur à
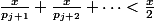
Si on écrit un tel

sous la forme
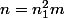
où

n'a aucun facteur carré, nous avons
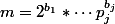
où les
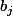
sont tous égaux à 0 ou 1. On a
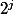
choix possibles pour les exposants et donc au plus
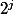
valeurs différentes de m. De plus nous avons
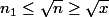
. Il y'a donc, au plus,

valeurs différentes de
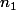
, ainsi :
 \geq 2^j\sqrt{x})
. On obtient en fait
 < 2^j\sqrt{x}, x < 2^{2j+2})
Or ceci est faux pour
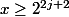
. Donc la série est divergente.
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 07 Déc 2008, 11:50
par Imod » 07 Déc 2008, 11:50
Si je ne m'abuse il s'agît de la démonstration d'Erdös telle qu'on peut la lire dans "Le Grand Livre" !
Imod
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 07 Déc 2008, 11:51
par Zweig » 07 Déc 2008, 11:51
Ce n'était pas précisé ...
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 07 Déc 2008, 11:53
par ffpower » 07 Déc 2008, 11:53
il a dit "Je ne vous demande pas de ressortir la démo d'Euler ou Erdos"...Cela dit je ne la connaissiat pas,donc c est bien de l avoir postée^^..Cela dit je prefere la demo d Euler
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 07 Déc 2008, 11:53
par acoustica » 07 Déc 2008, 11:53
Zweig a écrit:Du bouquin d'Hardy[/TEX]
Or ceci est faux pour
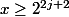
. Donc la série est divergente.
C'est quoi ce bouquin? Il a l'air bien! Si il est sur ordi, tu peux me l'envoyer? :happy2:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 07 Déc 2008, 11:54
par Zweig » 07 Déc 2008, 11:54
Bah écoute, quand j'ai rédigé la démo, je n'avais pas vu son message.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 07 Déc 2008, 11:54
par Zweig » 07 Déc 2008, 11:54
Il existe en effet une version numérisée de ce bouquin ... en anglais !
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 07 Déc 2008, 11:55
par acoustica » 07 Déc 2008, 11:55
Zweig a écrit:Il existe en effet une version numérisée de ce bouquin ... en anglais !
Encore mieux!
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 07 Déc 2008, 11:56
par Zweig » 07 Déc 2008, 11:56
Ok j't'envois ça en MP.
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 07 Déc 2008, 11:56
par acoustica » 07 Déc 2008, 11:56
Zweig a écrit:Ok j't'envois ça en MP.
Super merci!! :we: :we: :we:
Il est pas trop volumineux, il va passer?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
 . Donc
. Donc ) , le nombre d'entiers
, le nombre d'entiers 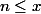 divisibles par au moins un des nombres
divisibles par au moins un des nombres 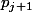 ,
, 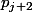 ,... est inférieur à
,... est inférieur à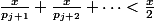
 sous la forme
sous la forme 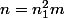 où
où  n'a aucun facteur carré, nous avons
n'a aucun facteur carré, nous avons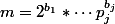 où les
où les 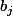 sont tous égaux à 0 ou 1. On a
sont tous égaux à 0 ou 1. On a 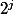 choix possibles pour les exposants et donc au plus
choix possibles pour les exposants et donc au plus 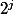 valeurs différentes de m. De plus nous avons
valeurs différentes de m. De plus nous avons 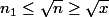 . Il y'a donc, au plus,
. Il y'a donc, au plus,  valeurs différentes de
valeurs différentes de 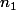 , ainsi :
, ainsi :  \geq 2^j\sqrt{x}) . On obtient en fait
. On obtient en fait  < 2^j\sqrt{x}, x < 2^{2j+2})
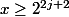 . Donc la série est divergente.
. Donc la série est divergente.