Sans faire trop de théorie... :
- Partant de
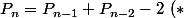\)
tu commence par regarder si, en posant
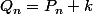
(k=cst) il n'y aurais pas moyen de se ramener à une vrai récurence
linéaire, c'est à dire sans le -2 à la fin.
Comme
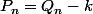
on a :
\ \Leftrightarrow\ Q_{n}-k=(Q_{n-1}-k)+(Q_{n-2}-k)-2\ \Leftrightarrow\ Q_{n}=Q_{n-1}+Q_{n-2}-2-k)
Donc il suffit de prendre
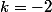
pour que ça marche.
- Ensuite, pour trouver l'expression de
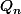
en fonction de

, on commence par ne pas tenir compte des condition initiales, mais par chercher des suites le plus simple possible vérifiant la relation
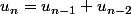
.
Si on "teste" une suite géométrique
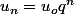
(avec

et

non nuls) on a :
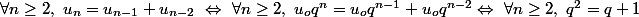
Formule dans laquelle il n'y a plus de n.
Il n'y a plus qu'à résoudfre cette équation du second degrés dont les solutions sont les fameux

et
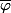
du post de chan79.
On constate ensuite que, non seulement les suites de la forme
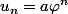
et
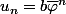
vérifient
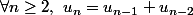
, mais que les suites de la forme
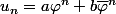
(

et

constante réelles quelconques) vérifient aussi la formule.
- On termine en cherchant quelles valeurs prendre pour

et pour

de façon à ce que les valeurs initiales soient bien égales à ce qu'on veut (donc ici on veut que
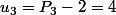
et
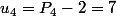
)
