Très très joli !!!
Une suggestion (juste le plan car c'est plutôt long et très pénible à écrire en Latex mon truc) :
A ) Lemme : si f'(x) -> 0 alors f(x)/x -> 0
TAF
B) on montre qu'on peut se ramener à a=0 en posant
 = x^a f(x))
On montre que g a les même propriétés en utilisant le lemme.
C) on écrit n+1 relation de Taylor-Lagrange
f(x) = somme de Taylor-Lagrange à l'ordre n+1
f(x+1) = somme de Taylor-Lagrange à l'ordre n+1
...
f(x+n) = somme de Taylor-Lagrange à l'ordre n+1
Ca fait un système de Vandermonde (en écrivant
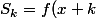-f(x) - k^{n+1} f^{n+1}(u_k)/(n+1)!)
= ...) qu'on sait inverser donc de manière indépendant de x. On sait exprimer les
/k!)
en fonction des
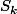
avec des coefficients constants. La conclusion suit.
C'est un truc comme ça Nightmare ? Y'a moyen de se passer des lemmes qui sont plutôt chts à montrer ??
