Equation fonctionnelle - Fonction du plan dans R
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 28 Déc 2010, 20:12
par Zweig » 28 Déc 2010, 20:12
Salut,
Soient

un point du plan et
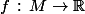
vérifiant pour tout

-gone régulier
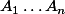
: [CENTER]
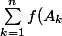 =0)
[/CENTER]
Que dire de

?
-
Anonyme
 par Anonyme » 28 Déc 2010, 20:47
par Anonyme » 28 Déc 2010, 20:47
Est ce qu'un triangle équilatéral est considéré comme un n-gone régulier ? (ou bien faut-il que n>3)
Si oui je pense pouvoir démontrer que f est identiquement nulle.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 28 Déc 2010, 20:50
par Zweig » 28 Déc 2010, 20:50
Oui, on parle de polygone à partir de
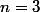
. Et oui, f est la fonction nulle.
-
Anonyme
 par Anonyme » 28 Déc 2010, 20:52
par Anonyme » 28 Déc 2010, 20:52
J'ai une solution en découpant un hexagone en triangles équilatéraux est ce la tienne ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 28 Déc 2010, 20:55
par Zweig » 28 Déc 2010, 20:55
Tu fais ça par récurrence ? Moi, je pars d'un point quelconque

du plan de sorte que
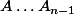
soit un

-gone régulier et j'envoie ce polygone sur

autres polygones (réguliers) par rotation de centre

et d'angle
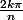
, pour tout
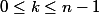
-
Anonyme
 par Anonyme » 28 Déc 2010, 21:27
par Anonyme » 28 Déc 2010, 21:27
Zweig a écrit:j'envoie ce polygone sur

autres polygones (réguliers)
k=n-1 non ?
Sinon j'ai pas trop compris ce que tu as fais ... peux tu développer un peu plus ?
blanc=a une image positive
noir= a une image négative
En ce qui me concerne j'ai pris deux points M1 et M2 blancs du plan. A partir de ces deux point je construis M tel que le triangle soit équilatéral. M3 est noir. Puis je construis M4 tel que le triangle M M2 M3 soit équilatéral. M3 est blanc. Je réitere le processus jusquà M6 et j'obtiens alors un hexagone M1 M2 ...M6 blanc ayant M pour centre. Et j'en déduis que tout ces points on nécessairement une image nulle.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
autres polygones (réguliers)