Entre un et deux

[azertytreza]

Salut

(bon après c'est peut être trop simple désolé si c'est connu , je ne connaissais pas)

en ce qui me concerne la démo me prend une page A4 en écrivant petit mais un pro fera ça en dix lignes maxi

en général question démo je suis nul (pas pro du tout)

On se place dans l'espace affine de dimension

muni de la distance euclidienne usuelle

Soient et deux droites quelconques

donc de sorte que et

alors on vérifie toujours

[GaBuZoMeu]

C'est visiblement faux.

[azertytreza]

oui il y a une coquille dans mon énoncé

(merde j'ai mal recopié ma feuille)

[azertytreza]

désolé j'ai mal recopié ma feuille

je voulais dire

[azertytreza]

Merci GaBuZoMeu

j'ai corrigé mon énoncé (la faute stupide de l'oublie d'un carré)

bon sinon pour expliquer le titre ("un ou deux " ) ma démo fait entre une et deux pages

je posterai ma démo plus tard

[GaBuZoMeu]

est plus joli (je trouve) en

qui devient évident quand on réalise que la quantité du milieu est . Pour ce faire, il est commode d'écrire

et de procéder de même pour .

[azertytreza]

Salut GaBuZoMeu

...toi tu est un pro(dans mon esprit c'est lumineux)

je suis certain que mon bidule en une page (soyons honnête deux pages ) toi tu le fais en dix lignes

et quand bien même en plus que ça bah pour moi vous êtes Dieu (majuscule , dire minuscule ça fait minable du genre le type qui veut pas se mouiller)

je posterai ma démo mais bon là j'ai un peu la flemme : je suis crevé là !

[azertytreza]

Salut GaBuZoMeu

Je posterai ma démo demain soir (je dois aller chez le vétérinaire pour mon chat)

En tout cas merci, le fait de savoir que c'est ok pour l'inégalité bah j'ai dormi huit heures d'affilées

ça à l'air con comme ça mais quand je me plante en maths (impossible de dormir et impossible de réfléchir froidement en ce qui me concerne)

bon là j'écoute de la zic je pourrais la faire cette nuit mais bon en fait mon cerveau ne suit pas le rythme là

encore merci

[azertytreza]

... la démo ( entre parenthèse je suis mort de rire, mais je ne dit pas pourquoi, ça se devine facilement)

je place des lignes pour signifier que chaque partie ainsi constituée servira plus loin

__________

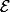
l'espace affine de dimension et sa direction

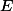
Il existe un point de tel que



__________





__________





________







_________

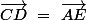
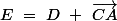
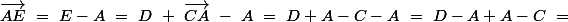
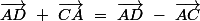
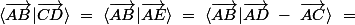
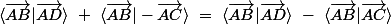
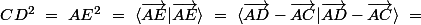
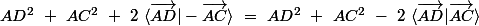
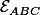
un sous espace affine de de direction

de dimension et qui possède les points

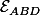
un sous espace affine de de direction

de dimension et qui possède les points

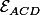
un sous espace affine de de direction

de dimension et qui possède les points

Dans les contextes de sous-espaces vectoriels de dimension et à propos d'un angle

engendré par et

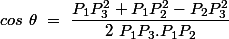
Al-Kashi dit et

________________

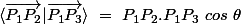
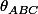
angle engendré par et

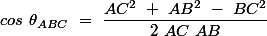
donc


________________

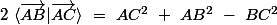
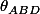
angle engendré par et

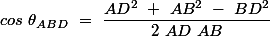
donc


________________

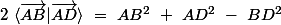
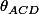
angle engendré par et

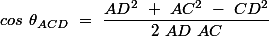
donc

________________





________________


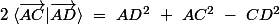
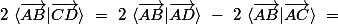
mais aussi un sous espace affine de de direction

de dimension et qui possède les points

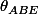
angle engendré par et

Al-Kashi dit

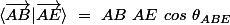
et comme





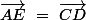
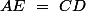
comme alors idem

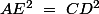
et idem





________________

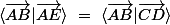
Al-Kashi dit :

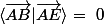
Si alors

_______________

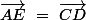
comme alors et sont colinéaires

et donc est un vecteur de

mais aussi

Euclide dit que si on discute des trois droites , ,

alors on discute de droites de

et comme ce sous espace affine est de dimension 2, bah il dit qu'on est entrain de discuter de droites d'un plan

et dans ce cas il dit :

si et si alors

et si et si alors

dans ce cas Al-Kashi dit que

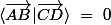
si alors

et du coup

__________________

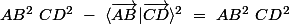
Al-Kashi dit aussi que

si alors et sont colinéaires

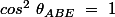
et il dit aussi que et aussi



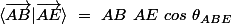
comme et sont colinéaires

si alors

et donc

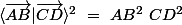
donc si si alors

________________________

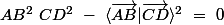
pour finir











et comme

[GaBuZoMeu]

De l'art de se compliquer la vie pour pas grand chose. Je rappelle que j'ai déjà donné plus haut une solution rapide :

et bien sûr

[azertytreza]

Bonjour GaBuZoMeu

bah oui (et ça confirme ma stupidité laquelle je n'ai jamais douté)

effectivement je ne pouvais pas poster une démo que je ne connaissais pas ni un résultat que je ne connaissais pas avant d'avoir fait ma démo et d'avoir ouvert ce sujet puis lire ta démo (et je ne pouvais copier ta démo non plus)

[beagle]

azerytreza
bienvenue sur un forum de partage!

ça donne envie de mettre des trucs perso, hein?

PS: j'ai connu maths forum avec un gars comme Doraki, il pliait les exos en deux lignes.
du concentré vindiou , c'était de la forte!Du brutal!
https://www.youtube.com/watch?v=btIkYYTFqDQ
Mais jamais il venait la ramener pour comparer, hierarchiser avec les autres approches.

PS: et le gars m'envoie un
" Tu n'as vraiment que ça à faire et à dire ?"
euh pas mieux, et toi?

[azertytreza]

ah non mais moi je ne me prend pas la tête (je suis ailleurs )

GaBuZoMeu a complètement raison

il n'y a pas de honte non plus

de toute façon j'étais bien obligé de poster ma démo sur la rubrique défi car celui qui ouvre est obligé d'avoir une démo sinon c'est pas la rubrique défi mais la rubrique question

[beagle]

"GaBuZoMeu a complètement raison "

et bien non!
Lorsque tu es agrégé, lorsque tu as ce niveau en math,
c'est complètement incompréhensible d'étaler sur les fils qu'il n' y a qu'une seule solution à un problème mathématique,
avec les ponctuations : "point barre", … "se compliquer la vie",... etc

C'est insupportable au niveau mathématique déjà,
et encore plus au niveau humain et relationnel…

Il faut lui faire remarquer, c'est lui rendre service.
Il ne va pas dire merci tout de suite néanmoins...

[azertytreza]

Bonjour Beagle

Dis tu ne crois pas que dans la vie il y a des choses plus graves ?

(moi mon chat est obligé de prendre un médoc matin et soir, alors très franchement je trouve que ça c'est mille fois plus problématique)

Je comprends les chamailleries ceci dit , c'est des trucs qu'on voit chez tous les pros mais bon moi je suis ailleurs

bon à plus les Camarades

[beagle]

Bah comme tu le dis ya plus grave,
mais certaines personnes viennent sur le forum comme élèves pour progresser,
d'autres viennent pour l'amour des maths, et ceux là n'ont pas à recevoir des notes d'anciens profs.

déjà en restant sur un plan mathématique, l'idée d'une solution unique est absurde,
l'idée d'une solution "la meilleure" peut dépendre du niveau de maths des intervenants.
Donc s'amuser à ça , déjà c'est puéril et mathématiquement inconsistant.

ensuite au niveau relationnel, les gens doivent venir en confiance, doivent poser leurs interrogations en confiance, c'est pourtant facile à comprendre, non?

[azertytreza]

Pour moi les mathématiciens auront la chance de survivre face aux machines (c'est leur destin)

Je conçois bien que des fois vous vous disputiez (et c'est même important )

Pour moi je vous considère comme les lions quand ils sont petits et qu'ils jouent entre eux pour s'entrainer mais plus tard vos dents seront celles qui broyeront l'humain car l'humain est condamné retourner sur son arbre

Après tout il en ait descendu juste pour vous mettre en place sur ce monde : il a joué son rôle , à présent qu'il retourne d'où il vient!

bon je dois partir travailler là ... à plus les camarades

[GaBuZoMeu]

Beagle : bien gentil de te poser en père-la-morale, mais il vaudrait mieux parler de la réalité au lieu de te laisser mener par ta rancoeur. Où ai-je écrit que la solution que j'ai donnée était la seule possible ? Et, très franchement, trouves-tu la solution écrite par azertytreza raisonnable ? As tu vraiment lu ce fil ?

[azertytreza]

j'ai du travail là mais bon moi je vois que GaBuZoMeu a raison et que peut-on faire quand quelqu'un a raison ?

bah rien!

Ceci dit de répète que j'admets que les pros se chamaillent , on voit ça dans tous les corps de métier c'est culturel et accepté de tous et j'espère bien que cette chamaillerie en fait partie(vu de l'extérieur c'est pas évident à le savoir non plus)

Où ai-je écrit que la solution que j'ai donnée était la seule possible ?

nul part!

Et, très franchement, trouves-tu la solution écrite par azertytreza raisonnable ?

non !

bon je retourne à mon travail !

à plus tous

[beagle]

"Où ai-je écrit que la solution que j'ai donnée était la seule possible ?"

puisque azertytreza répond , alors j'argumente.
Dans ce fil de discussion, là , non.

Dans d'autres fils de discussions clairement oui
Lorsque l'on donne sa solution et on ponctue "point barre",
lorsqu'on établit une relation d'ordre sur les réponses alors il est clair que l'on souhaite dire qu'il existe une solution, la meilleure forcément,
là où les autres solutions sont juste adaptées au niveau d'un interlocuteur donné.

Et ne pas dire les pros se chamaillent. je ne suis pas pro en maths, j'ai un excellent niveau fin de collège je pense en maths …, pas plus!