Salut,
Je suis entièrement d'accord avec Skullkid. Pourquoi on a appelé les nombres racines de polynômes non existants dans R des complexes ? Parce qu'ils étaient complexés par leur différence ???
Je ne vais pas dire : en math, on n'utilise jamais de complexes, on utilise uniquement une extension des nombres réels construite à partir de l'instanciation de la solution à l'équation x²+1 = 0, sous prétexte que la définition de complexe est : compliqué/difficile à comprendre (ou même carrément "Ensemble structuré d'éléments mnésiques inconscients de la personnalité, qui l'organisent nécessairement chez chacun, à l'insu ou non du sujet, et déterminent ses affects et ses actions.")...
Et en quoi Pi est plus réel que "i" ? Surtout quand on sait que e(i*pi) = -1. Pour moi, "i" a autant de réalité que la coordonnés y d'un point dans un plan.
L'infini [erratum : l'infini effectif] n'existe pas (réflexi
60 messages
- Page 3 sur 3 - 1, 2, 3
par nodjim » 20 Mar 2015, 20:56
J'ai lu il n'y a pas longtemps "l'axiome de l'infini". Je ne savais pas que ça existait. Si les axiomeurs ont créé ça, je pense que c'est parce que c'est un outil devenu indispensable dans bien des domaines des maths.
Donc, oui on pourrait à la rigueur ne pas s'en servir.
Les maths sont aujourd'hui axiomatisées. Il faut faire avec ces règles. Je me suis fait atomisé il y a peu de temps quand j'ai voulu remettre en cause des résultats en rapport avec l'infini, parce que je n'avais pas pris la peine de bien regarder les axiomes liés à ces notions d'infini (théorie des ensembles, théorie des nombres,...). Et pourtant j'étais sûr de moi.
Donc, oui on pourrait à la rigueur ne pas s'en servir.
Les maths sont aujourd'hui axiomatisées. Il faut faire avec ces règles. Je me suis fait atomisé il y a peu de temps quand j'ai voulu remettre en cause des résultats en rapport avec l'infini, parce que je n'avais pas pris la peine de bien regarder les axiomes liés à ces notions d'infini (théorie des ensembles, théorie des nombres,...). Et pourtant j'étais sûr de moi.
par Robic » 21 Mar 2015, 07:01
Skullkid a écrit:La question est toujours la même : pourquoi donc, dans la vertigineuse escalade conceptuelle que constitue la construction des mathématiques, es-tu réfractaire uniquement à l'étape où on prononce pour la première fois le mot "infini" ?
Ce n'est pas ça, le problème. Je ne suis réfractaire à rien. Je dis juste que lorsqu'en maths on "croit" utiliser l'infini, en fait ce n'est pas le cas. Comme le disait Leon1789 que tu citais, « tout énoncé sur l'infini est la traduction d'un énoncé sur le fini. »
Pourquoi devrait-on se faire un devoir de systématiquement remplacer "infini" par quelque chose comme "comportement de [...] quand [...] augmente", sans se donner la peine de remplacer "réel" par "classe d'équivalence de suites de Cauchy rationnelles" ?
Il ne faut surtout pas faire ça, ce serait trop lourd à gérer ! Mais il ne faut pas oublier que c'est le cas.
Le problème se réduit donc uniquement au fait que tu n'aimes pas l'infini, soit (comme je le pense) parce qu'il se heurte à l'idée préexistante que tu t'en fais, soit parce que tu as du mal à saisir les maths qui sont derrière (ce qui ne semble pas être le cas vu que tu es visiblement capable de comprendre des constructions relativement chiadées).
Le problème, c'est plutôt :
- que je ne me suis pas fait comprendre ;
- que je ne remettais pas en cause les maths, ni la perception que les mathématiciens ont des maths (Leon1789 n'est pas dupe et toi non plus puisque tu le cites), mais la perception qu'ont "certaines personnes" des maths (pas les pros). (J'ai déjà lu des phrases du genre : l'analyse est la science de l'infini... non : des limites.)
De plus j'avoue que je ne m'étais jamais trop posé de questions sur les réels, que je prenais en gros pour des nombres à développement décimal illimité (je savais que c'était les limites des suites de rationnels, mais en gros). Quand j'étais étudiant on m'a montré la méthodes des coupures, que je n'ai pas retenue (je me souviens du mot, mais ça n'avais jamais servi), et il a fallu cette discussion pour que je me rende compte que je ne savais pas ce qu'étaient les nombres réels. Maintenant je sais (je crois). J'en conclus que se poser ce genre de question peut être utile.
Benjamin a écrit:Pourquoi on a appelé les nombres racines de polynômes non existants dans R des complexes ?
Pour le mot "complexe", je ne sais pas, mais en tout pour ces nombres je ne vois aucun mystère tant qu'on ne fait pas croire qu'il existe i tel que i²=-1 et c'est tout (oui, il existe, mais il faut le construire, pas seulement prétendre qu'il existe). Les nombres complexes sont des couples de nombres pour lesquels on a étendu les opérations usuelles de façon à conserver leurs propriétés (distributivité, tout ça) ; par exemple i est la notation de (0,1) et en effet (0,1)x(0,1) = (-1,0). D'ailleurs je ne comprends pas pourquoi on n'enseigne pas cette définition (je sais qu'on peut aussi les définir avec des matrices mais je ne connais pas et je soupçonne que ça doit revenir au même).
Nodjim a écrit:J'ai lu il n'y a pas longtemps "l'axiome de l'infini". Je ne savais pas que ça existait. Si les axiomeurs ont créé ça, je pense que c'est parce que c'est un outil devenu indispensable dans bien des domaines des maths.
Il n'y a pas d'infini dans l'axiome de l'infini. Cet axiome dit juste qu'il existe un ensemble ayant la propriété que si on prélève des éléments dedans, il en restera nécessairement. On est à nouveau dans le « tout énoncé sur l'infini est la traduction d'un énoncé sur le fini. » Et c'était ça mon message.
(Mais de cette discussion j'en ai retenu, entre autres, qu'il est possible que certains domaines que je ne connais pas utilisent "vraiment" l'infini.)
par nodjim » 21 Mar 2015, 11:14
"De plus j'avoue que je ne m'étais jamais trop posé de questions sur les réels, que je prenais en gros pour des nombres à développement décimal illimité"
Ce n'est pas non plus une erreur de représenter les réels comme tels, je cois. Certes, ce n'est pas forcément la plus pratique ni la plus aboutie.
Ce n'est pas non plus une erreur de représenter les réels comme tels, je cois. Certes, ce n'est pas forcément la plus pratique ni la plus aboutie.
par Robic » 21 Mar 2015, 15:02
Oui, en fait ce que je voulais dire était plutôt : je croyais qu'il suffisait de considérer les nombres réels comme des développements décimaux illimités pour les avoir compris.
par zygomatique » 21 Mar 2015, 21:41
salut
bon j'ai presque tout lu l'énoncé initial ... et le reste en diagonale ...
entre autre j'ai vu : on pourrait dire que l'exponentielle est un polynome
et c'est la que je réponds ce qui a déjà été dit : en math il n'y a que des ensembles
exp appartient à un ensemble de fonctions qui contient lui même l'ensemble des fonctions polynômes dont une suite a pour limite exp ....
pi appartient à un ensemble de nombres qui contient lui même un ensemble de nombres (rationnels) dont une (au moins) suite a pour limite pi ....
la théorie des catégories montre bien que l'unique objet des mathématiques c'est de mettre chaque objet mathématique dans une boite contenant tous les objets ayant même propriétés, les boites pouvant elles-mêmes s'inclure, "s'intersecter" ....
et pourquoi cela ?
parce que quand je prends un objet de telle boite alors je sais que objet vérifie les propriétés ceci et cela et je peux manipuler ces propriétés pour produire des/d'autres vérités ....
car l'objet de la mathématique c'est de produire des vérités ...
j'aurais encore à dire mais j'arrête là .... sur une note d'humour ....
l'infini c'est comme ma retraite :: un véritable mirage :: plus je m'en approche plus elle s'éloigne .... :ptdr:
bon j'ai presque tout lu l'énoncé initial ... et le reste en diagonale ...
entre autre j'ai vu : on pourrait dire que l'exponentielle est un polynome
et c'est la que je réponds ce qui a déjà été dit : en math il n'y a que des ensembles
exp appartient à un ensemble de fonctions qui contient lui même l'ensemble des fonctions polynômes dont une suite a pour limite exp ....
pi appartient à un ensemble de nombres qui contient lui même un ensemble de nombres (rationnels) dont une (au moins) suite a pour limite pi ....
la théorie des catégories montre bien que l'unique objet des mathématiques c'est de mettre chaque objet mathématique dans une boite contenant tous les objets ayant même propriétés, les boites pouvant elles-mêmes s'inclure, "s'intersecter" ....
et pourquoi cela ?
parce que quand je prends un objet de telle boite alors je sais que objet vérifie les propriétés ceci et cela et je peux manipuler ces propriétés pour produire des/d'autres vérités ....
car l'objet de la mathématique c'est de produire des vérités ...
j'aurais encore à dire mais j'arrête là .... sur une note d'humour ....
l'infini c'est comme ma retraite :: un véritable mirage :: plus je m'en approche plus elle s'éloigne .... :ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par Robic » 22 Mar 2015, 10:54
entre autre j'ai vu : on pourrait dire que l'exponentielle est un polynome
Tu as bien vu que je disais que c'était ridicule, n'est-ce pas ? L'idée était de dire : si on croit qu'un espace vectoriel de dimension infinie est un espace vectoriel dans lequel les objets ont une infinité de coordonnées, alors on aurait des combinaisons linéaires infinies, ce qui est un non sens (qui mènerait à considérer l'exponentielle comme un polynôme).
et c'est la que je réponds ce qui a déjà été dit : en math il n'y a que des ensembles
C'est ce qu'on dit mais est-ce ce qu'on fait ? Par exemple lorsqu'on étudie des équations différentielles on dit que f appartient à
par zygomatique » 22 Mar 2015, 14:37
oui bien sur ...
justement étudier les propriétés des objets permet de classer ces objets et de les mettre dans différentes boites ....
justement étudier les propriétés des objets permet de classer ces objets et de les mettre dans différentes boites ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par Rha » 22 Mar 2015, 16:37
Bonjour,
Pour apporter une pierre au débat concernant ensembles et propriétés.
Deux différences entre propriétés et ensembles en mathématiques:
-Les propriétés sont des énoncés d'un langage fixé et il y a une limite à ce que ce langage peut décrire comparé à ce que dont il peut prouver l'existence.
Certaines choses que l'on voudrait exprimer comme des propriétés ne sont a priori pas facilement exprimables:
Pour chaque réel
par exemple, la propriété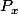 
: "être égal à " existe-t-elle? Pas sûr, n'est-ce pas?
-Certaines propriétés ne définissent pas un objet de l'univers (ensemble), sans quoi la théorie se contredirait:
Par exemple, la propriété "avoir exactement un élément".
Quant à l'utilité de l'axiome de l'infini, je pense qu'elle apparaît lorsqu'on veut considérer des structures "d'ordre élevé". Par exemple, il n'est pas sûr qu'on puisse formuler une propriété "être un réel" qui soit telle que la collection des ensembles la satisfaisant se comporte comme l'ensemble des réels sans faire appel à l'axiome de l'infini.
Il devient alors compliqué de montrer des propriétés assez élémentaires comme "entre deux rationnels positifs distincts on trouve toujours une puissance
-ième d'un rationnel". (je ne dis pas qu'il est impossible de le montrer sans axiome de l'infini).
Même si l'on se réduit à considérer des théorèmes portant sur des ensembles finis, le passage par des ensembles infinis permet de montrer les choses plus facilement. (comparaison des complexités des preuves analytiques et arithmétiques d'énoncés arithmétiques)
Pour rejoindre Robic sur un point, je pense qu'il faut se méfier de l'intuition qui fait croire que les types d"infini sont des types de grandeur d'ensembles dont les "tailles" seraient incommensurables.
Quant à la question de l'infini actuel et l'infini potentiel, je me demande si ces deux notions sont vraiment distinctes, ou si au contraire on ne peut pas considérer l'infini de
comme potentiel.
Pour apporter une pierre au débat concernant ensembles et propriétés.
Deux différences entre propriétés et ensembles en mathématiques:
-Les propriétés sont des énoncés d'un langage fixé et il y a une limite à ce que ce langage peut décrire comparé à ce que dont il peut prouver l'existence.
Certaines choses que l'on voudrait exprimer comme des propriétés ne sont a priori pas facilement exprimables:
Pour chaque réel
-Certaines propriétés ne définissent pas un objet de l'univers (ensemble), sans quoi la théorie se contredirait:
Par exemple, la propriété "avoir exactement un élément".
Quant à l'utilité de l'axiome de l'infini, je pense qu'elle apparaît lorsqu'on veut considérer des structures "d'ordre élevé". Par exemple, il n'est pas sûr qu'on puisse formuler une propriété "être un réel" qui soit telle que la collection des ensembles la satisfaisant se comporte comme l'ensemble des réels sans faire appel à l'axiome de l'infini.
Il devient alors compliqué de montrer des propriétés assez élémentaires comme "entre deux rationnels positifs distincts on trouve toujours une puissance
Même si l'on se réduit à considérer des théorèmes portant sur des ensembles finis, le passage par des ensembles infinis permet de montrer les choses plus facilement. (comparaison des complexités des preuves analytiques et arithmétiques d'énoncés arithmétiques)
Pour rejoindre Robic sur un point, je pense qu'il faut se méfier de l'intuition qui fait croire que les types d"infini sont des types de grandeur d'ensembles dont les "tailles" seraient incommensurables.
Quant à la question de l'infini actuel et l'infini potentiel, je me demande si ces deux notions sont vraiment distinctes, ou si au contraire on ne peut pas considérer l'infini de
par Robic » 22 Mar 2015, 17:19
Il me semble évident que l'infini de N est potentiel, d'ailleurs c'est inscrit dans leur construction, non ? (À partir du successeur : on donne une loi pour construire n+1 à partir de n, je crois). Pour considérer que l'infini de N est actuel, je crois qu'il faudrait pouvoir parcourir N dans l'autre sens, en descendant.
Peut-être qu'il y a des infinis actuels en maths, mais je n'en suis pas convaincu pour les notions de base.
Comme je comprends le truc, x est une classe d'équivalence de suites de Cauchy rationnelles, donc cette propriété exprime que deux classés d'équivalence sont égales, donc qu'elles ont les même représentants.
Je n'ai pas compris pourquoi tu dis que la propriété "avoir exactement un élément" mène à une contradiction. (Au fait, les ensembles à un élément ne sont-ils pas les représentants de la classe d'équivalence qui définit l'entier 1 ? - L'idée vient de me venir à l'instant : les entiers ne seraient-ils pas définis par des classes d'équivalence par rapport à la relation « peut être mis en bijection avec » ? Il faut que je vérifie ça...) (Du coup les réels seraient des classes d'équivalence de classes d'équivalence...)
-----
Je reviens après avoir consulté l'article de Wikipédia sur le sujet, où les entiers sont construits autrement (selon la méthode dont j'avais entendu parler avec les successeurs). Dans l'article il est dit que « L'axiome de l'infini est nécessaire pour assurer l'existence d'un ensemble contenant tous les entiers naturels. » Je crois que je saisis ce qui coince chez moi : je ne vois aucun intérêt à considérer l'existence d'un tel ensemble, sinon comme écriture pratique (« soit n dans N » au lieu de « soit n entier naturel »).
Chaque fois qu'on utilise des entiers naturels, par exemple comme indices de suite, on n'a pas besoin de la totalité, juste d'un nombre aussi grand qu'on veut. Il ne faut donc pas s'assurer l'existence d'une infinité d'entiers, mais l'existence d'autant d'entiers qu'on veut, ce qui est assuré par le processus itératif avec les successeurs.
Peut-être que ça sert dans des branches très abstraites ? Mais cet axiome me paraît non nécessaire pour les maths basiques (le programme de licence, disons).
D'ailleurs je pense à un truc (maintenant que j'ai lu la réponse de Monsieur23 dans le sujet sur les nombres ordinaux) : si on a dû mettre comme axiome l'existence d'un ensemble stable par successeur (donc un infini actuel - j'avais mal compris cet axiome lors de mes précédentes interventions), c'est que l'infini actuel est quelque chose qu'on doit se forcer à admettre. Et mon tout premier message pourrait se résumer à : je crois que l'axiome de l'infini ne sert pas autant qu'on le dit en maths (OK dans des branches très abstraites, disons).
Tiens, et en cherchant des infos sur l'axiome de l'infini je tombe sur cette page : https://fr.vikidia.org/wiki/Infini_%28math%C3%A9matiques%29 qui traite de l'infini potentiel et de l'infini actuel. Hop, je retourne lire tout ça...
- « Plus exactement, il est possible de définir une théorie des ensembles parfaitement cohérente qui affirmerait que tous les ensembles seraient finis. » Aah ! :zen:
- « Mais elle serait peu intéressante. » Ooh ! :hum:
(D'un côté un fait, de l'autre un jugement de valeur...)
Peut-être qu'il y a des infinis actuels en maths, mais je n'en suis pas convaincu pour les notions de base.
Pour chaque réel x par exemple, la propriété P_x: "être égal à x" existe-t-elle? Pas sûr, n'est-ce pas?
Comme je comprends le truc, x est une classe d'équivalence de suites de Cauchy rationnelles, donc cette propriété exprime que deux classés d'équivalence sont égales, donc qu'elles ont les même représentants.
Je n'ai pas compris pourquoi tu dis que la propriété "avoir exactement un élément" mène à une contradiction. (Au fait, les ensembles à un élément ne sont-ils pas les représentants de la classe d'équivalence qui définit l'entier 1 ? - L'idée vient de me venir à l'instant : les entiers ne seraient-ils pas définis par des classes d'équivalence par rapport à la relation « peut être mis en bijection avec » ? Il faut que je vérifie ça...) (Du coup les réels seraient des classes d'équivalence de classes d'équivalence...)
-----
Je reviens après avoir consulté l'article de Wikipédia sur le sujet, où les entiers sont construits autrement (selon la méthode dont j'avais entendu parler avec les successeurs). Dans l'article il est dit que « L'axiome de l'infini est nécessaire pour assurer l'existence d'un ensemble contenant tous les entiers naturels. » Je crois que je saisis ce qui coince chez moi : je ne vois aucun intérêt à considérer l'existence d'un tel ensemble, sinon comme écriture pratique (« soit n dans N » au lieu de « soit n entier naturel »).
Chaque fois qu'on utilise des entiers naturels, par exemple comme indices de suite, on n'a pas besoin de la totalité, juste d'un nombre aussi grand qu'on veut. Il ne faut donc pas s'assurer l'existence d'une infinité d'entiers, mais l'existence d'autant d'entiers qu'on veut, ce qui est assuré par le processus itératif avec les successeurs.
Peut-être que ça sert dans des branches très abstraites ? Mais cet axiome me paraît non nécessaire pour les maths basiques (le programme de licence, disons).
D'ailleurs je pense à un truc (maintenant que j'ai lu la réponse de Monsieur23 dans le sujet sur les nombres ordinaux) : si on a dû mettre comme axiome l'existence d'un ensemble stable par successeur (donc un infini actuel - j'avais mal compris cet axiome lors de mes précédentes interventions), c'est que l'infini actuel est quelque chose qu'on doit se forcer à admettre. Et mon tout premier message pourrait se résumer à : je crois que l'axiome de l'infini ne sert pas autant qu'on le dit en maths (OK dans des branches très abstraites, disons).
Tiens, et en cherchant des infos sur l'axiome de l'infini je tombe sur cette page : https://fr.vikidia.org/wiki/Infini_%28math%C3%A9matiques%29 qui traite de l'infini potentiel et de l'infini actuel. Hop, je retourne lire tout ça...
- « Plus exactement, il est possible de définir une théorie des ensembles parfaitement cohérente qui affirmerait que tous les ensembles seraient finis. » Aah ! :zen:
- « Mais elle serait peu intéressante. » Ooh ! :hum:
(D'un côté un fait, de l'autre un jugement de valeur...)
par Rha » 22 Mar 2015, 20:00
Si je te donne un réel particulier, comme 
, 
, 
, tu pourras avec un peu de travail trouver une propriété qu'il est seul à vérifier. Mais existe-t-il une telle propriété pour tout réel? Difficile à dire.
La propriété "avoir exactement 1 élément" ne correspond pas à un ensemble: il n'existe pas d'ensemble contenant exactement tous les ensembles à 1 élément. (car sinon sa réunion serait l'ensemble de tous les ensembles, dont l'existence est contradictoire)
Sache que sans axiome de l'infini, il n'y a pas d'ensemble des entiers naturels, donc pas de suites de rationnels, donc pas de suites de Cauchy de rationnels. Pas sûr donc qu'on puisse disposer de la classe des réels.
Voici un modèle de la théorie finie des ensembles, c'est-à-dire de ZFC où on a remplacé l'axiome de l'infini par sa négation (ce qui fait que tout ensemble y est en bijection avec un ordinal fini):
L'ensemble de base est l'ensemble des parties finies de, et la relation d'appartenance est interprétée par la relation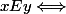 
 \in y)
où  = \sum \limits_{n \in x} 2^n)
.** (
est une bijection de l'ensemble des parties finies de dans ).
Dans ce modèle, il semble difficile de définir les réels. Mais c'est peut-être possible, je ne sais pas. En tout cas tu peux essayer au moins pour te rendre compte que ce n'est pas évident.
**Si tu préfères, tu peux considérer le modèle alternatif suivant)
où  \in \mathbb{N}^2, x E' y \Longleftrightarrow x \in \varphi^{-1}(y))
.
est un isomorphisme de 
-structures entre ces deux modèles.
La propriété "avoir exactement 1 élément" ne correspond pas à un ensemble: il n'existe pas d'ensemble contenant exactement tous les ensembles à 1 élément. (car sinon sa réunion serait l'ensemble de tous les ensembles, dont l'existence est contradictoire)
Sache que sans axiome de l'infini, il n'y a pas d'ensemble des entiers naturels, donc pas de suites de rationnels, donc pas de suites de Cauchy de rationnels. Pas sûr donc qu'on puisse disposer de la classe des réels.
Voici un modèle de la théorie finie des ensembles, c'est-à-dire de ZFC où on a remplacé l'axiome de l'infini par sa négation (ce qui fait que tout ensemble y est en bijection avec un ordinal fini):
L'ensemble de base est l'ensemble des parties finies de
Dans ce modèle, il semble difficile de définir les réels. Mais c'est peut-être possible, je ne sais pas. En tout cas tu peux essayer au moins pour te rendre compte que ce n'est pas évident.
**Si tu préfères, tu peux considérer le modèle alternatif suivant
par Robic » 22 Mar 2015, 20:06
Rha a écrit:Mais existe-t-il une telle propriété pour tout réel? Difficile à dire.
OK, je comprends.
La propriété "avoir exactement 1 élément" ne correspond pas à un ensemble
Ah, donc la notion de propriété est plus forte que la notion d'ensemble ! :zen:
Sache que sans axiome de l'infini, il n'y a pas d'ensemble des entiers naturels, donc pas de suites de rationnels, donc pas de suites de Cauchy de rationnels. Pas sûr donc qu'on puisse disposer de la classe des réels.
Il n'y a pas d'ensemble des entiers naturels, mais il y a des entiers naturels, et autant qu'on veut. Donc il y a des rationnels, et il y a des suites (a priori finies) de Cauchy de rationnels, ces suites étant définies pour les termes 0 à n, n étant aussi grand qu'on veut (donc finies mais illimitées, donc utilisables pour calculer des limites).
par zygomatique » 22 Mar 2015, 21:57
i est un nombre bien réel ....
puisque multiplier par i c'est tourner d'un quart de tour .... et que je sache tout le monde peut tourner d'un quart de tour ... et ce n'est pas si complexe que ça de tourner d'un quart de tour ....
:ptdr: :ptdr:
au fait :: on a plus l'air d'être dans le forum "café pédagogique" mais plutôt dans le forum "gnole pédagogique" ....
:ptdr: :ptdr:
je ne sais plus qui disait (peut-être Einstein) "Dieu est le plus court chemin de 0 à l'infini (dans un sens comme dans l'autre) ...
en tout cas quand j'ai été frapper à la porte du paradis on m'a répondu "ya personne" !!!
:ptdr: :ptdr:
puisque multiplier par i c'est tourner d'un quart de tour .... et que je sache tout le monde peut tourner d'un quart de tour ... et ce n'est pas si complexe que ça de tourner d'un quart de tour ....
:ptdr: :ptdr:
au fait :: on a plus l'air d'être dans le forum "café pédagogique" mais plutôt dans le forum "gnole pédagogique" ....
:ptdr: :ptdr:
je ne sais plus qui disait (peut-être Einstein) "Dieu est le plus court chemin de 0 à l'infini (dans un sens comme dans l'autre) ...
en tout cas quand j'ai été frapper à la porte du paradis on m'a répondu "ya personne" !!!
:ptdr: :ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par Rha » 23 Mar 2015, 00:19
Peux-tu définir la propriété "être de Cauchy" pour une suite finie?
L'ensemble des suites finies de rationnels est dénombrable, donc tu ne peux tout simplement pas définir tous les réels avec. Il y aurait quelques nuances à apporter mais bon. L'idée est qu'il n'existe pas de moyen uniforme de définir chaque réel à partir de quantités finies de données.
Note que si tu connais une suite, par exemple la suite des puissances de deux, tu peux la coder par une formule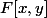
signifiant 
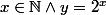, et tu peux alors vérifier si oui ou non la "suite" représentée par 
est de Cauchy. Mais tu ne définis pas ainsi un objet mathématique (ensemble) pour lequel on pourrait appliquer les théorèmes de la théorie des ensembles. Par ailleurs, tu ne pourras pas a priori trouver une formule pour définir chaque suite de rationnels. (c'est un peu la même histoire que le truc avec les 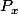de tout à l'heure, et cela rejoint ce que j'ai dit avant; même si je dois avouer que l'explication et la présentation rigoureuse de ce phénomène m'échappent)
L'ensemble des suites finies de rationnels est dénombrable, donc tu ne peux tout simplement pas définir tous les réels avec. Il y aurait quelques nuances à apporter mais bon. L'idée est qu'il n'existe pas de moyen uniforme de définir chaque réel à partir de quantités finies de données.
Note que si tu connais une suite, par exemple la suite des puissances de deux, tu peux la coder par une formule
par Robic » 23 Mar 2015, 13:07
Tu me poses une très bonne question et c'est en effet ce qui m'a tracassé depuis hier soir.
Voici l'idée que j'ai en tête. Lorsqu'on dit qu'une suite (Un) tend vers zéro, on veut dire par là que pour tout
, aussi petit qu'on veut, il existe un rang N à partir duquel tous les indices qui suivent N produisent un terme inférieur à ce . Dit comme ça, je suis en train de parler d'une infinité d'indice. Mais ce n'est pas nécessaire, il suffit de dire les choses autrement : il existe un rang N à partir duquel si je choisis un n quelconque (donc fini), et si de plus n > N, alors le n-ème terme de la suite sera plus petit que . Cette fois, je n'ai pas eu besoin d'invoquer la totalité des indices supérieurs à N. Leur infinité n'est que potentielle.
On peut procéder de même pour définir une suite de Cauchy : il existe un rang N à partir duquel si je choisis p et q, et si de plus p et q sont plus grands que N, alors etc. etc.
Maintenant, le problème, c'est que je ne sais plus ce qu'est une suite. Comme tu dis, si on peut définir la suite par une formule, la question est réglée, mais il ne faut pas considérer que c'est le cas de toute suite (je pense même qu'on doit pouvoir démontrer que ça n'existe pas, la potentialité des formules ne pouvant pas être mise en bijection avec la potentialité des suites irrationnelles). J'ai envie de définir une suite de cette façon : « on appelle suite de nombres la donnée de n nombres pour n quelconque aussi grand qu'on veut. » Non, ça ne va pas, n a l'air fixé, or il ne doit pas l'être. « On appelle suite de nombres une application qui, pour tout entier n, associe un nombre. Du coup il faut que je définisse une application sans utiliser l'axiome de l'infini, houlà... Et il faut une définition qui permette de distinguer deux suites, je ne peux pas me permettre une définition vague du genre « une suite est un truc que, quand on se donne un indice entier, alors on peut toujours lui associer un nombre ». Cela dit, il n'est pas nécessaire de recourir à l'axiome de l'infini pour distinguer deux suites : deux suites U et V sont différentes s'il existe un indice n tel que Un différent de Vn. Le problème se pose juste pour la définition...
Mince, on ne va quand même pas s'obliger à admettre l'axiome de l'infini juste pour définir des suites, alors qu'ensuite, pour les utiliser, on ne s'en sert plus - il manquerait plus que ça !
Il faudrait que je réfléchisse un peu plus à tout ça...
(Je suis à deux doigts d'admettre l'axiome de l'infini pour des choses aussi simples que les suites, eh bien ça me dérange beaucoup plus que, par exemple, la fois où j'ai entendu parler du théorème de Gödel.)
Voici l'idée que j'ai en tête. Lorsqu'on dit qu'une suite (Un) tend vers zéro, on veut dire par là que pour tout
On peut procéder de même pour définir une suite de Cauchy : il existe un rang N à partir duquel si je choisis p et q, et si de plus p et q sont plus grands que N, alors etc. etc.
Maintenant, le problème, c'est que je ne sais plus ce qu'est une suite. Comme tu dis, si on peut définir la suite par une formule, la question est réglée, mais il ne faut pas considérer que c'est le cas de toute suite (je pense même qu'on doit pouvoir démontrer que ça n'existe pas, la potentialité des formules ne pouvant pas être mise en bijection avec la potentialité des suites irrationnelles). J'ai envie de définir une suite de cette façon : « on appelle suite de nombres la donnée de n nombres pour n quelconque aussi grand qu'on veut. » Non, ça ne va pas, n a l'air fixé, or il ne doit pas l'être. « On appelle suite de nombres une application qui, pour tout entier n, associe un nombre. Du coup il faut que je définisse une application sans utiliser l'axiome de l'infini, houlà... Et il faut une définition qui permette de distinguer deux suites, je ne peux pas me permettre une définition vague du genre « une suite est un truc que, quand on se donne un indice entier, alors on peut toujours lui associer un nombre ». Cela dit, il n'est pas nécessaire de recourir à l'axiome de l'infini pour distinguer deux suites : deux suites U et V sont différentes s'il existe un indice n tel que Un différent de Vn. Le problème se pose juste pour la définition...
Mince, on ne va quand même pas s'obliger à admettre l'axiome de l'infini juste pour définir des suites, alors qu'ensuite, pour les utiliser, on ne s'en sert plus - il manquerait plus que ça !
Il faudrait que je réfléchisse un peu plus à tout ça...
(Je suis à deux doigts d'admettre l'axiome de l'infini pour des choses aussi simples que les suites, eh bien ça me dérange beaucoup plus que, par exemple, la fois où j'ai entendu parler du théorème de Gödel.)
par Doraki » 23 Mar 2015, 13:35
Pour ce qui est de rejeter l'axiome de l'infini, je sais pas trop ce qu'on peut construire sans l'utiliser.
Déjà on ne peut pas construire N donc on ne peut pas construire la fonction successeur ou l'addition (comme des éléments de l'univers). (par contre par des formules oui, mais c'est assez lourdingue)
Une suite de rationnels chez moi c'est une fonction de N dans Q.
Donc pour en parler t'es obligé de pouvoir parler de N. Si tu parles SEULEMENT de suites finies ben tu ne peux rien faire puisque tu ne peux pas parler de limite d'une suite finie.
Tu ne peux pas dire qu'une suite converge vers pi en regardant seulement 1000 termes de la suite.
C'est une notion qui dépend de tous les termes à la fois.
Déjà on ne peut pas construire N donc on ne peut pas construire la fonction successeur ou l'addition (comme des éléments de l'univers). (par contre par des formules oui, mais c'est assez lourdingue)
Une suite de rationnels chez moi c'est une fonction de N dans Q.
Donc pour en parler t'es obligé de pouvoir parler de N. Si tu parles SEULEMENT de suites finies ben tu ne peux rien faire puisque tu ne peux pas parler de limite d'une suite finie.
Tu ne peux pas dire qu'une suite converge vers pi en regardant seulement 1000 termes de la suite.
C'est une notion qui dépend de tous les termes à la fois.
par Robic » 23 Mar 2015, 13:54
Je ne vois pas en quoi l'axiome de l'infini est nécessaire pour construire les entiers. Avec la fonction successeur, on les construit de proche en proche, donc lorsqu'on parle d'entier aussi grand qu'on veut, ça veut dire qu'on va utiliser la fonction successeur et qu'on l'applique autant de fois qu'on veut. Mais à aucun moment je n'ai besoin de la totalité des entiers.
Pour ce qui concerne les suites, il est clair qu'il ne faut pas raisonner en suites finies. J'ai envie de raisonner en suites illimitées, c'est-à-dire dont on peut choisir un terme aussi grand qu'on veut mais sans pour autant manipuler la totalité des termes. Mais je ne vois pas trop comment définir ça pour l'instant sans l'axiome de l'infini. J'ai le sentiment que ça doit être possible, c'est pour ça qu'il faut que j'y réfléchisse encore. Je veux bien croire que j'ai tort, mais j'ai besoin d'en être persuadé.
Pour ce qui concerne les suites, il est clair qu'il ne faut pas raisonner en suites finies. J'ai envie de raisonner en suites illimitées, c'est-à-dire dont on peut choisir un terme aussi grand qu'on veut mais sans pour autant manipuler la totalité des termes. Mais je ne vois pas trop comment définir ça pour l'instant sans l'axiome de l'infini. J'ai le sentiment que ça doit être possible, c'est pour ça qu'il faut que j'y réfléchisse encore. Je veux bien croire que j'ai tort, mais j'ai besoin d'en être persuadé.
par Rha » 23 Mar 2015, 18:19
Il va être difficile de se persuader d'une telle chose, car le problème n'est pas clairement posé.
Tu peux te demander si dans un modèle de la théorie finie des ensembles, tu peux trouver ou non une classe d'objets et des pseudos fonctions* qui vues extérieurement comme des ensembles et des vraies applications (mais interprétées dans le modèle) forment un corps commutatif totalement ordonné archimédien et complet.
A mon avis, trouver un exemple ou un contre exemple est très difficile.
Je crois que David Hilbert et d'autres après lui se sont intéressés à des formalisations du finitisme et ont étudié leurs portées. J'ai un vague souvenir d'avoir lu quelque chose de vague comme "blabla montrent que la plupart des raisonnements mathématiques de tous les jours, y compris ceux de l'arithmétique et d'une partie de l'analyse peuvent être menés selon une approche finitiste". Cela m'avait surpris mais je n'avais pas cherché plus de détail à ce moment. Il est peut-être temps. Je reviendrai avec des liens si je trouve quelque chose d'intéressant.
*formules fonctionnelles portant sur un domaine qui ne forme pas un ensemble mais une classe propre, comme la fonction cardinal
Tu peux te demander si dans un modèle de la théorie finie des ensembles, tu peux trouver ou non une classe d'objets et des pseudos fonctions* qui vues extérieurement comme des ensembles et des vraies applications (mais interprétées dans le modèle) forment un corps commutatif totalement ordonné archimédien et complet.
A mon avis, trouver un exemple ou un contre exemple est très difficile.
Je crois que David Hilbert et d'autres après lui se sont intéressés à des formalisations du finitisme et ont étudié leurs portées. J'ai un vague souvenir d'avoir lu quelque chose de vague comme "blabla montrent que la plupart des raisonnements mathématiques de tous les jours, y compris ceux de l'arithmétique et d'une partie de l'analyse peuvent être menés selon une approche finitiste". Cela m'avait surpris mais je n'avais pas cherché plus de détail à ce moment. Il est peut-être temps. Je reviendrai avec des liens si je trouve quelque chose d'intéressant.
*formules fonctionnelles portant sur un domaine qui ne forme pas un ensemble mais une classe propre, comme la fonction cardinal
par Robic » 23 Mar 2015, 19:30
Ta réponse est très intéressante (notamment « blabla montrent que... » ! En tout cas je commence à me faire à l'idée que l'axiome de l'infini est nécessaire pour définir certaines choses (pour les suites, je ne vois plus comment s'en passer, mais ça ne prouve rien) même si les « maths de tous les jours » n'y font pas appel. Je trouve intéressant de se pencher sur la question. Oui, visiblement c'est Hilbert qui prônait le finitisme donc il doit avoir plein de choses à dire à ce sujet...
par mathelot » 23 Mar 2015, 20:12
Skullkid a écrit:es-tu réfractaire uniquement à l'étape où on prononce pour la première fois le mot "infini" ? Sachant que ce mot est introduit en suivant rigoureusement les mêmes règles logiques que celles qui ont permis d'introduire des mots tels que "nombre relatif" et "nombre rationnel".
en ce qui me concerne, c'est Mr Debiard, mon prof de maths en 1ereS , qui l'a prononcé pour la première fois pour "décorer" le tableau de variation d'une fonction croissante. Evidemment, qu'un tel concept , l'infini, serve à décorer les tableaux de variation relève de l'imposture intellectuelle (?).
le jour où l'on consacrera un mois d'étude à 'l'intro du concept de l'infini en 1ère, les maths et leur didactique auront bien progressé....surtout que dans le même temps, ma prof de physique ne distinguait pas
les pseudos forces (façon Coriolis) des forces de la physique, comme électricité et magnétisme.
Aujourd'hui chez G*bert jeune, j'ai pu consulter le tome I de "Mécanique" de Feynmann
c'est un vrai régal.
60 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :