Raisonnement par récurrence math
18 messages
- Page 1 sur 1
 raisonnement par récurrence math
raisonnement par récurrence math
besoin d'aide !!!!!
on utilise le raisonnement par récurrence montrer que :
pour tout n de N*, 3 divise le nombre 4n^3-n
on utilise le raisonnement par récurrence montrer que :
pour tout n de N*, 3 divise le nombre 4n^3-n
Modifié en dernier par imaneaawiou le 04 Déc 2020, 14:10, modifié 1 fois.
Re: raisonnement par récurrence math
[quote="imaneaawiou"]besoin d'aide !!!!!
on utilise le raisonnement par récurrence montrer que :
pour tout n de N*, 3 divise le nombre 4n^3-n
on utilise le raisonnement par récurrence montrer que :
pour tout n de N*, 3 divise le nombre 4n^3-n
Re: raisonnement par récurrence math
BONJOUR !
Qu'as-tu essayé ? On te dit de raisonner par récurrence, c'est une grosse indication. Qu'as-tu essayé pour suivre cette indication ?
Qu'as-tu essayé ? On te dit de raisonner par récurrence, c'est une grosse indication. Qu'as-tu essayé pour suivre cette indication ?
Re: raisonnement par récurrence math
oui j'ai essayée (j'ai fait toutes les étapes: verification ,supposition..)mais je ne suis pas sûre du résultat
Modifié en dernier par imaneaawiou le 04 Déc 2020, 16:33, modifié 1 fois.
Re: raisonnement par récurrence math
démontrer par récurrence ce n'est pas trouver une solution
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: raisonnement par récurrence math
premiere chose à faire, verifier l'initiation
verifier que c'est bon pour n=1
deuxieme chose à faire,l'hérédité,
tu considère que si 4n^3-n est multiple de 3
alors on aura 4(n+1)^3 - (n+1) qui sera aussi multiple de 3
donc principe de base tu pars de 4n^3-n
et tu essayes d'arriver au cas n+1
par exemple ici on a que cela se termine par n
tu voudrais toi avoir du -(n+1)
ben tu rajoute du -1,
en ajoutant 3 =4 -1
alors 4n^3+ 4 -(n+1) est divisible par 3
4(n^3+1) - (n+1) divisible par 3
...on y est presque
verifier que c'est bon pour n=1
deuxieme chose à faire,l'hérédité,
tu considère que si 4n^3-n est multiple de 3
alors on aura 4(n+1)^3 - (n+1) qui sera aussi multiple de 3
donc principe de base tu pars de 4n^3-n
et tu essayes d'arriver au cas n+1
par exemple ici on a que cela se termine par n
tu voudrais toi avoir du -(n+1)
ben tu rajoute du -1,
en ajoutant 3 =4 -1
alors 4n^3+ 4 -(n+1) est divisible par 3
4(n^3+1) - (n+1) divisible par 3
...on y est presque
Modifié en dernier par beagle le 04 Déc 2020, 16:45, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: raisonnement par récurrence math
mathelot a écrit:Bonjour,
On utilise l'identité (a+b)^3=a^3+3a^2b+3ab^2+b^3
mercii
j ai trouvée 3(k+4n^2+4n+3) et c est logique
Re: raisonnement par récurrence math
on aimerait etre persuadé que la logique du raisonnement par récurrence soit là aussi.
tu peux nous rassurer?
et donc l'écrire un peu...
tu peux nous rassurer?
et donc l'écrire un peu...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: raisonnement par récurrence math
beagle a écrit:premiere chose à faire, verifier l'initiation
verifier que c'est bon pour n=1
deuxieme chose à faire,l'hérédité,
tu considère que si 4n^3-n est multiple de 3
alors on aura 4(n+1)^3 - (n+1) qui sera aussi multiple de 3
donc principe de base tu pars de 4n^3-n
et tu essayes d'arriver au cas n+1
par exemple ici on a que cela se termine par n
tu voudrais toi avoir du -(n+1)
ben tu rajoute du -1,
en ajoutant 3 =4 -1
alors 4n^3+ 4 -(n+1) est divisible par 3
4(n^3+1) - (n+1) divisible par 3
...on y est presque
j ai fait toutes ces étapes
et j ai trouvée 3(k+4n^2+4n+3)
et c est logique
merci à vous.
Re: raisonnement par récurrence math
je me permets de rajouter que trouver un truc dans le raisonnement par récurrence,
c'est pour moi incompréhensible,
si n alors n+1, je comprends ...
c'est pour moi incompréhensible,
si n alors n+1, je comprends ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: raisonnement par récurrence math
et le jour où l'initiation ne marchera pas,
ben tu auras démontré un truc complètement faux
ben tu auras démontré un truc complètement faux
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: raisonnement par récurrence math
beagle a écrit:on aimerait etre persuadé que la logique du raisonnement par récurrence soit là aussi.
tu peux nous rassurer?
et donc l'écrire un peu...
pour n=1 on a : 4×1^3-1=3
donc la proposition est vraie pour n=1
on suppose que soit n appartient à N*: 4n^3-n=3k k appartient à N
et on montre que : 4(n+1)^3 - (n+1)=3k'
4(n+1)^3 - (n+1)=4(n^3+3n^2+3n+1)-(n+1)
=4n^3+12n^2+12n+3
=3k+12n^2+12n+3
=3(k+4n^2+4n+3)
=3k'
donc pour tout n de N* 3 divise le nombre 4n^3 - n
Re: raisonnement par récurrence math
Il y a une faute à la deuxième ligne de calcul. Je te laisse vérifier.
Re: raisonnement par récurrence math
imaneaawiou a écrit:beagle a écrit:on aimerait etre persuadé que la logique du raisonnement par récurrence soit là aussi.
tu peux nous rassurer?
et donc l'écrire un peu...
pour n=1 on a : 4×1^3-1=3
donc la proposition est vraie pour n=1
on suppose que soit n appartient à N*: 4n^3-n=3k k appartient à N
et on montre que : 4(n+1)^3 - (n+1)=3k'
4(n+1)^3 - (n+1)=4(n^3+3n^2×1+3n×1^2+1^3)-(n+1)
=4(n^3+3n^2+3n+1)-(n+1)
=4n^3+12n^2+12n+3
=3k+12n^2+12n+3
=3(k+4n^2+4n+3)
=3k'
donc pour tout n de N* 3 divise le nombre 4n^3 - n
Re: raisonnement par récurrence math
GaBuZoMeu a écrit:Il y a une faute à la deuxième ligne de calcul. Je te laisse vérifier.
j ai modifiée la 2eme linge
c ça la faute?
Re: raisonnement par récurrence math
Il y a toujours une faute, maintenant à la troisième ligne. Surveille le coefficient de n.
Re: raisonnement par récurrence math
soit pour 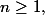 on définit
on définit  par
par 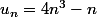
Pour n >0
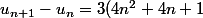)
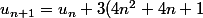)
donc si est divisible par 3,
est divisible par 3,  itou.
itou.
Pour n >0
donc si
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
