Bonjour a tous,
En admis l'existence d'un carré négatif donc l'existence de i.
Alors
Soit le nombre X tel que X<1 et X>1 avec X#1
Et le nombre Z tel que Z<-1 et Z>-1 avec Z#-1
Les deux nombres X et Z se retrouve hors l'ensemble de réel avec cette définition comme le cas du nombre i.
Est ce que X et Z existent comme i.
Que peut on dire sur X et Z?
Un nouveau type de nombre
14 messages
- Page 1 sur 1
Re: Un nouveau type de nombre
La définition de X et Z montre que X et Z n'appartiennent pas a R.
Et l'utilisation de <> Dans cette définition montre que X et Z n'appartiennent pas a C.
Alors X et Z ne sont pas réel ni complexe.
Et l'utilisation de <> Dans cette définition montre que X et Z n'appartiennent pas a C.
Alors X et Z ne sont pas réel ni complexe.
Re: Un nouveau type de nombre
Alors où sont-ils ?
On admet l'existence de i au lycée mais il existe des méthodes pour lui donner un sens. Ce n'est pas parce que quelque chose n'est pas défini qu'il suffit de le nommer pour qu'il existe. Par exemple tu as toujours su que 1/0 n'existe pas et jusqu'à présent aucun mathématicien ne travaille avec un nombre qui serait 1/0 (les puristes m'épargneront les anneaux de caractéristique 1).
Si tu veux une construction élémentaire de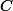 :
:
On pose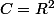 (le plan) et pour deux vecteurs
(le plan) et pour deux vecteurs 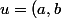, v=(c,d)) je pose
je pose 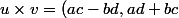) . Voilà : les nombres complexes c'est l'ensemble
. Voilà : les nombres complexes c'est l'ensemble 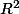 muni de la somme usuelle et du produit de deux vecteurs que je viens de définir et i c'est le vecteur
muni de la somme usuelle et du produit de deux vecteurs que je viens de définir et i c'est le vecteur ) et
et 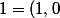) (le 1 de C n'est pas le même 1 que celui de R).
(le 1 de C n'est pas le même 1 que celui de R).
On vérifie que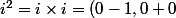=(-1,0)=-1) .
.
Maintenant à ton tour. Si tu veux me convaincre de l'existence de ces deux nombres, définis-les .
.
Pour ça tu dois te demander ce qu'est "<". Si tu utilises la définition usuelle pour le définir (à l'aide d'une relation d'ordre) tes nombres ne peuvent pas exister car ils contredisent les axiomes que doit vérifier une relation d'ordre (en particulier l'axiome qui s'appelle antisymétrie).
On admet l'existence de i au lycée mais il existe des méthodes pour lui donner un sens. Ce n'est pas parce que quelque chose n'est pas défini qu'il suffit de le nommer pour qu'il existe. Par exemple tu as toujours su que 1/0 n'existe pas et jusqu'à présent aucun mathématicien ne travaille avec un nombre qui serait 1/0 (les puristes m'épargneront les anneaux de caractéristique 1).
Si tu veux une construction élémentaire de
On pose
On vérifie que
Maintenant à ton tour. Si tu veux me convaincre de l'existence de ces deux nombres, définis-les
 .
.Pour ça tu dois te demander ce qu'est "<". Si tu utilises la définition usuelle pour le définir (à l'aide d'une relation d'ordre) tes nombres ne peuvent pas exister car ils contredisent les axiomes que doit vérifier une relation d'ordre (en particulier l'axiome qui s'appelle antisymétrie).
Re: Un nouveau type de nombre
il n'y a pas de contradiction de dire que X>1 et X<1 pour un réel ça veux dire que X=1
le problème viens de faite de dire que X est différent de 1 donc je peux les utiliser.
le problème viens de faite de dire que X est différent de 1 donc je peux les utiliser.
Re: Un nouveau type de nombre
Ici en trouve bien l'utilité de ses nombres pour représenter la somme de cette série Étrange que en peux démontrer ça divergente et aussi ca convergente .
cafe-mathematique/series-theorem-t204357.html#p1345991
cafe-mathematique/series-theorem-t204357.html#p1345991
Re: Un nouveau type de nombre
Le problème c'est que tu ne comprends pas qu'on ne peut pas définir X comme tu l'as fait. Pour définir un objet il faut dire dans quel espace il est. C'est ce qu'Archytas à fait pour te montrer comment on construit i.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Un nouveau type de nombre
Zou37 a écrit:Bonjour a tous,
En admis l'existence d'un carré négatif donc l'existence de i.
Alors
Soit le nombre X tel que X<1 et X>1 avec X#1
Et le nombre Z tel que Z<-1 et Z>-1 avec Z#-1
Les deux nombres X et Z se retrouve hors l'ensemble de réel avec cette définition comme le cas du nombre i.
Est ce que X et Z existent comme i.
Que peut on dire sur X et Z?
On peut dire que X et Z existent, ça c'est clair. Mais ils n'existent pas comme i. L'existence de i est due à l'absence ou l'impossibilité de savoir comparer le vide avec zéro. Mais depuis qu'on a introduit les différentes puissances du vide, on s'est trouvé confronté à la difficulté majeure de la comparaison de celle-ci avec zéro. C'est tout simplement pour cela que X et Y existent, mais dans un univers supérieur à i. Mais vu la complexité du sujet, sur ce forum c'est assez compliqué de développer ce sujet passionnant!
Re: Un nouveau type de nombre
Dans l'article 14-21 , p37- 48, journal de Yk & -SL. Mais attention c'est de la haute voltige.
Et ça dépasse mon niveau, tu as pu le voir ici. Se mettre à la hauteru de Yk & SL c'est pas facile.
Pour l'adresse: c'est Yk & SL, rue Simon Cussonnet , Tussorel (Eure).
Et ça dépasse mon niveau, tu as pu le voir ici. Se mettre à la hauteru de Yk & SL c'est pas facile.
Pour l'adresse: c'est Yk & SL, rue Simon Cussonnet , Tussorel (Eure).
Re: Un nouveau type de nombre
Merci j'ai cherché sur google j'ai rien trouver.
Et je suis en chomage je n'ai meme pas un pc ou tel et j'utilise ceux de la famille et amis parfois donc pas le temps de trop chercher.
Et je suis en chomage je n'ai meme pas un pc ou tel et j'utilise ceux de la famille et amis parfois donc pas le temps de trop chercher.
Re: Un nouveau type de nombre
@Zou37 : comme on l'as dis à plusieurs reprise ce n'est pas possible de "définir" tes Y et Z ainsi.
Aviateur ne fait que de se moquer.
Aviateur ne fait que de se moquer.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Un nouveau type de nombre
Je sais j'ai vu que c'était une blague sur Google.
Moi aussi je fais juste une blague je sais que il reste plus rien a dire en mathématiques ou en physique.
https://forums.futura-sciences.com/deba ... sique.html
Moi aussi je fais juste une blague je sais que il reste plus rien a dire en mathématiques ou en physique.
https://forums.futura-sciences.com/deba ... sique.html
Re: Un nouveau type de nombre
@Sylviel
Du coup tu peux te servir du fil que Zou37 vient de citer ainsi que de celui-ci (indice, extrazlove = Zou37) pour le crucifier à tout jamais. C'est le genre de mec qui utilise ses idées farfelues pour balancer des contre-vérités, dire qu'il vient du futur, que la science est insuffisante et que la religion c'est trop cool etc.
Du coup tu peux te servir du fil que Zou37 vient de citer ainsi que de celui-ci (indice, extrazlove = Zou37) pour le crucifier à tout jamais. C'est le genre de mec qui utilise ses idées farfelues pour balancer des contre-vérités, dire qu'il vient du futur, que la science est insuffisante et que la religion c'est trop cool etc.
Re: Un nouveau type de nombre
Sake a écrit:@Sylviel
Du coup tu peux te servir du fil que Zou37 vient de citer ainsi que de celui-ci (indice, extrazlove = Zou37) pour le crucifier à tout jamais. C'est le genre de mec qui utilise ses idées farfelues pour balancer des contre-vérités, dire qu'il vient du futur, que la science est insuffisante et que la religion c'est trop cool etc.
Je viens de le dégager.
Un peu marre de ses conneries...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
