
Un autre examen pour discussion ^^
30 messages
- Page 1 sur 2 - 1, 2
probleme !
Exo 2 :
1- il faut qu'on trouve une fonction g(x) qui réalise : g(0) = g (1)
f'(c) = 3/2 . 1/racine(1+3c)
On pose : g(x) = f(x) - Primitive de {3/2 . 1/racine(1+3c)}
comment ??
1- il faut qu'on trouve une fonction g(x) qui réalise : g(0) = g (1)
f'(c) = 3/2 . 1/racine(1+3c)
On pose : g(x) = f(x) - Primitive de {3/2 . 1/racine(1+3c)}
comment ??
Bonjour.
Inutile de se casser la tête, la fonction=x+1) vérifie les condition
vérifie les condition =1) ,
, =2) et pour
et pour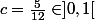 , on a
, on a \sqrt{1+3c}=2\sqrt{1+3c}=3) . Il est inutile d'appliquer le théorème de Rolle.
. Il est inutile d'appliquer le théorème de Rolle.
Encore une autre=1+\sqrt{x}) avec
avec 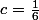
et une autre=1+x\sqrt{x}) , avec
, avec 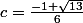
On peut maintenant à partir d'une solution trouvée construire une infinité d'autres, il suffit pour cela d'ajouter à une fonction
une fonction  nulle en
nulle en  , en
, en  et dont la dérivée s'annule au point
et dont la dérivée s'annule au point  trouvé associée à
trouvé associée à 
Pour=x+1) , on avait trouvé
, on avait trouvé 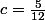 , on prend
, on prend (x-\frac{5}{12})^2h(x))
ZacklRyzuzaki a écrit:on a f'(c) sa primitive est f(c) alors on la remplace par f(x), mais il faut aussi trouver la primitive de {3/2 . 1/racine(1+3c)} ?? ^^
Inutile de se casser la tête, la fonction
Encore une autre
et une autre
On peut maintenant à partir d'une solution trouvée construire une infinité d'autres, il suffit pour cela d'ajouter à
Pour
ZacklRyzuzaki a écrit:on a f'(c) sa primitive est f(c) alors on la remplace par f(x), mais il faut aussi trouver la primitive de {3/2 . 1/racine(1+3c)} ?? ^^
Je ne comprends pas ta remarque.
La fonction g que je te propose vérifie bien les hypothèses tu théorème que l'énoncé te demande d'utiliser (je te laisse t'en assurer)
Ensuite, dérive g.
Le théorème te dit qu'il existe c tel que g'(c)=0
La conclusion s'obtient alors facilement.
(Remarque : dans ton énoncé je suppose qu'il faut remplacer LA fonction numérique par UNE fonction numérique)
Les 3 fonctions que j'ai données au début ni celles que j'ai données après ne sont pas obtenues en utilisant le théorème de Rolle, on peut y remédier en considérant la fonction  définie par
définie par =f(x)-\frac{x(x-c)^2u(x)}{(1-c)^2 u(1)}-1) où
où  est une fonction continue sur
est une fonction continue sur  et dérivable dans ]0,1[ et
et dérivable dans ]0,1[ et  la valeur trouvée associée à
la valeur trouvée associée à 
Pour=x+1) prendre
prendre =x+1-\frac{x(x-c)^2 u(x)}{(1-c)^2 u(1)}-1) avec c=\frac(5}{12}.
avec c=\frac(5}{12}.
Remarque:
La réponse que j'ai donnée ne correspond pas à l'énoncé de de l'exercice mais à celui-la:
Trouver des fonctions f continues sur [0,1], dérivables dans ]0,1[ telle que=1) ,
, =2) et vérifiant il existe
et vérifiant il existe 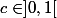 tel que
tel que \sqrt{1+3c}=3) et ce en utilisant la théorème de Rolle
et ce en utilisant la théorème de Rolle
L'énoncé commence par: Soit la fonction, je viens de prouver l'existence d'une infinité de fonctions répondant à l'énoncé initial de l'exo.
Pour
Remarque:
La réponse que j'ai donnée ne correspond pas à l'énoncé de de l'exercice mais à celui-la:
Trouver des fonctions f continues sur [0,1], dérivables dans ]0,1[ telle que
L'énoncé commence par: Soit la fonction, je viens de prouver l'existence d'une infinité de fonctions répondant à l'énoncé initial de l'exo.
deltab a écrit:Bonsoir.
Considérons les fonctions,
, toutes vérifient
et
.
Considérons la fonction
Montrons que l'équationadmet au moins une solution
dans ]0,1[, il suffit pour cela que
pour tout
. Il suffit donc de prendre
pour
Pour l'application du théorème de Rolle, lui associer la fonction V correspondante
Mais comment on va savoir que f(x) est égal exactement à x^(alpha+1) + 1 ??
ZacklRyzuzaki a écrit:Mais comment on va savoir que f(x) est égal exactement à x^(alpha+1) + 1 ??
Tu n'as qu'à faire les calculs et je n'ai pas dit que c'étaient les SEULES. et de plus elles répondent à mon énoncé pas au tien, il est temps de revoir son énoncé. (On t'avait la remarque dans ton autre topic)
Ton énoncé parlait de LA FONCTION et ça, ça suppose qu'il n'y en a qu'une seule
ZacklRyzuzaki a écrit:peut être que j'ai pas compris peut-tu expliquer suivant le théorème de Rolle stv ?
on ne peut se comprendre si on ne parle pas du même théorème de Rolle (s'il y'en a plusieurs). Celui que je connais est:
Soit
ZacklRyzuzaki a écrit:peut être que j'ai pas compris peut-tu expliquer suivant le théorème de Rolle stv ?
Je t'ai donné précédemment (à 19h11 hier) un cheminement pour résoudre le problème en utilisant Rolle, l'as tu lu ?
D'autre part, en me répétant : je pense que ton énoncé est mal recopié et qu'il faut remplacer LA par UNE
Bonjour
Je sais que le message ne m'est pas adressé.
Je voulais juste expliquer ma démarche.
1) Je trouve une fonction) (sans paramètre
(sans paramètre  ) vérifiant les conditions données sauf celle de l'existence de
) vérifiant les conditions données sauf celle de l'existence de  tel que ......
tel que ......
2) Pour cette fonction f, montrer l'existence d'un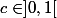 vérifiant l'équation
vérifiant l'équation \sqrt{1+3c}-3=0) et ce via le TVI appliqué à la fonction
et ce via le TVI appliqué à la fonction \sqrt{1+3x}-3) . Il est inutile d'appliquer le TVI sur l'intervalle [0,1], il suffit de l'appliquer à un sous-intervalle
. Il est inutile d'appliquer le TVI sur l'intervalle [0,1], il suffit de l'appliquer à un sous-intervalle 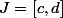 de
de  .
.
3) Construire la fonction) comme décrit plus haut pour pouvoir utiliser le théorème le Rolle.
comme décrit plus haut pour pouvoir utiliser le théorème le Rolle.
Ce n'est qu'après tout ce bric-à-brac que j'ai pensé à introduit un paramètre et considérer une famille
et considérer une famille ) tel que
tel que =f_0(x)) ,
, ) vérifie les conditions nécessaires et de l'idée que
vérifie les conditions nécessaires et de l'idée que 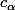 est une fonction continue de
est une fonction continue de  .
.
Pour le premier jet, je me suis basé sur la fonction=x+1) et poser ensuite
et poser ensuite =x^{\alpha+1}+1)
J'ai trouvé une autre fonction à savoir
à savoir =sin(\pi x)/2) +1) et
et =(sin(\pi x)/2) )^{\alpha+1}+1) avec
avec 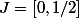
Thomas Joseph a écrit:D'autre part, en me répétant : je pense que ton énoncé est mal recopié et qu'il faut remplacer LA par UNE
Je sais que le message ne m'est pas adressé.
Je voulais juste expliquer ma démarche.
1) Je trouve une fonction
2) Pour cette fonction f, montrer l'existence d'un
3) Construire la fonction
Ce n'est qu'après tout ce bric-à-brac que j'ai pensé à introduit un paramètre
Pour le premier jet, je me suis basé sur la fonction
J'ai trouvé une autre fonction
deltab a écrit:on ne peut se comprendre si on ne parle pas du même théorème de Rolle (s'il y'en a plusieurs). Celui que je connais est:
Soitune fonction continue sur
, dérivable dans
telle que
. Il existe
telle que
Je suis d'accord avec tes remarques ...
Le théorème de Rolle que tu donnes est cependant plus restrictif qu'il ne devrait l'être, je pense.
Pour moi, c'est :
Soit
:zen:
Bonjour.
Le fait de prendre f(a)=f(b))=0 ne nuit en rien à la généralité. Pour ta version, je prend la fonction g(x)=f(x)+K et on a bien g(a)=g(b)=K et g'(x)=f'(x) d'où l'existence de c tel que g'(c)=0 et je peux faire le chemin inverse en prenant g(x)=f(x)-f(a).
Black Jack a écrit:Je suis d'accord avec tes remarques ...
Le théorème de Rolle que tu donnes est cependant plus restrictif qu'il ne devrait l'être, je pense.
Pour moi, c'est :
Soitune fonction continue sur
, dérivable dans
telle que
. Il existe
telle que
:zen:
Le fait de prendre f(a)=f(b))=0 ne nuit en rien à la généralité. Pour ta version, je prend la fonction g(x)=f(x)+K et on a bien g(a)=g(b)=K et g'(x)=f'(x) d'où l'existence de c tel que g'(c)=0 et je peux faire le chemin inverse en prenant g(x)=f(x)-f(a).
30 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
