Suites de fonctions, discussion

[Hyp]

Bonjour,

Je débute en séries de fonctions et j'aimerais avoir un petit éclaircissement sur un point que je comprends pas tout à fait (concernant déjà les suites de fonctions).

En étudiant la convergence simple de quelques suites de fonctions il arrive très souvent que l'on discute la convergence en quelques points particuliers. Et justement, je ne sais pas exactement quand est ce que la discussion s'impose.
Mon prof m'a dit brièvement que cette discussion a pour but d'éviter quelques formes mal définies en faisant tendre n vers l'infini par la suite.

Ce serait aimable que l'on m'explique ce point sur un exemple, et merci =)

[fatal_error]

salut,

en fait si tu poses
, ca sous entend que F(x) existe. Autrement dit que F(x) admet une limite finie en x.


Au lieu d'étudier , on étudie
On obtient une série en fonction de N, puis apres on fait tendre vers l'infini.

Exemple :
la série

Maintenant, si on pose , on a

On voit qu'il faut discuter le cas ou x=0.(sinon, riemann avec n^2)
on étudie alors
Ici, on voit qu'on a la serie divergente eq a ln. on ne peut donc pas écrire


De meme, on peut pas écrire
car qui est divergente. Ou alors, on précise que l'ensemble de def de F est {0}
J'espère avoir répondu à ta question

[Hyp]

Merci beaucoup pour l'explication mais j'ai peur qu'il n'y ait un petit malentendu =x.

La question est peut être plus simple que cela. Je sais que certaines notations de séries doivent vérifier quelques conditions pour avoir un sens, mais je parle plutôt de suites de fonctions (au sens propre).

par exemple, pour étudier la convergence de sur 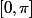, quelles sont les valeurs à étudier séparément et pourquoi ?
Encore désolé si je me suis mal exprimé au début.

[Purrace]

Tu peux par exemple regarder les valeurs en 0 et pi meme si ça a pas trop d'importance sur cet exemple ,puisque la limite simple est immédiate et démontre la CVu sur [a,pi] a>0.

Edit: j'avais pas vu le x en haut , en fait ta la cvu sur [0;pi]

[fatal_error]

re,

désolé, j'avais mal lu.


Ici, les x "chauds" sont 0, et pi. Quand tu fais tendre n vers l'infini, tu vois que nxexp(-nx) tend vers 0, pour
J'ai envie de dire qu'on cherche les valeurs ou ya des maximums ou des minimum, mais ca n'engage que moi.

Donc du coup, on traite le cas "normal":

le cas x=0,

le cas pi:


Si par exemple, on s'était intéressés a lintervalle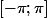 , il aurait fallu séparer l'intervalle en deux, a cause de l'exponentielle.
ben en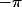 , on aurait supposer la divergence alors qu'en fait .

[Hyp]

Merci pour les réponses,

Ce que j'ai compris en gros est que cette discussion a pour but de lever l'indétermination des valeurs "chaudes" de x (de la forme ici), c'est bien ça ?

[mathelot]

Bjr,

Pour x fixé, quand on regarde la convergence simple,

on étudie une série numérique , c'est à dire une suite.

On applique des critères de convergence (Cauchy,D'alembert,comparaison avec une intégrale,Raabe-Duhamel,..) Sans doute , les valeurs de x que tu évoque viennent naturellement dans la discussion. ce sont des valeurs pour lequelles les critères ne marchent plus.

Par exemple, la série de ln(1+x) converge normalement sur tout compact
, converge en x=1 (cas particulier) et diverge en x=-1.