Determiner toutes les fonctions
Merci d'avance !!
Equation fonctionnelle !
4 messages
- Page 1 sur 1
Equation fonctionnelle !
par barbu23 » 13 Aoû 2007, 16:59
Bonjour:
Determiner toutes les fonctions
telles que :
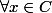
:  = a_{2}.f(x)^{2}+a_{1}.f(x)+a_{0}.f(1) $)
: L'ensemble des nombres complexes.
sont trois scalaires fixés dans .
Merci d'avance !!
Determiner toutes les fonctions
Merci d'avance !!
par kazeriahm » 13 Aoû 2007, 17:29
a mon avis il faut raisonner sur les racines du polynome en question après avoir calculé f(0)
euh ?
l'identité est solution, j'en vois pas d'autre (ou alors je vois mal)
euh ?
l'identité est solution, j'en vois pas d'autre (ou alors je vois mal)
par barbu23 » 13 Aoû 2007, 17:55
On considère 
les deux racines de 
, et 
les deux racines de ^{2}+a_{1}.f(x)+a_{0}.f(1) $)
...
Pas besoin de les calculer, n'est ce pas ?!...
Donc, on aboutit à la relation suivante :
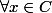
: (x-\alpha_{2})) = a_{2} (f(x) - \beta_{1})(f(x)-\beta_{2}) $)
Donc:
 = a_{2} (f(\alpha_{1}) - \beta_{1})(f(\alpha_{1})-\beta_{2}) = a_{2} (f(\alpha_{2}) - \beta_{1})(f(\alpha_{2})-\beta_{2}) $)
Pas besoin de les calculer, n'est ce pas ?!...
Donc, on aboutit à la relation suivante :
Donc:
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :