Pour Chaa13
82 messages
- Page 2 sur 5 - 1, 2, 3, 4, 5
par zermel0 » 03 Oct 2012, 22:03
toujours ce problème de variable...
n est un nombre, comme 100 ou 2.
2n ça reste n+n, etc... comme 200 = 100 + 100.
Tu le manipules comme si c'était un nombre comme les autres.
C'est juste pour dire "ce sera vrai avec tous les nombres" qu'on note n, sinon on devrait écrire "c'est vrai avec 1, avec 2, avec 3 ... etc" et ce, à l'infini...
n est un nombre, comme 100 ou 2.
2n ça reste n+n, etc... comme 200 = 100 + 100.
Tu le manipules comme si c'était un nombre comme les autres.
C'est juste pour dire "ce sera vrai avec tous les nombres" qu'on note n, sinon on devrait écrire "c'est vrai avec 1, avec 2, avec 3 ... etc" et ce, à l'infini...
par chaa13 » 03 Oct 2012, 22:23
Mon idée etait de de tout d'abord partie sur la base de :
Donc bon j'ai trouvé que la somme pour n qui est variant : (je mais ca sous forme de fonction)  =\frac{n}{2} * (n+1))
Donc maintenant je cherche pour n-1
par zermel0 » 03 Oct 2012, 22:33
Charles pour la seconde somme tu feras attention que son k est en fait un i hein
par chaa13 » 03 Oct 2012, 23:52
Argh je suis mort ! Si pour le 2. tu vouler bien dire ca : ))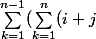
J'ai eu une petite aide de Zermel0 disant qui y'avait un nombre que était constant (Sinon je me barrer a perpet je croyais que les 2 nombre etait constant ...) Donc a partir de la j'ai réussi a avoir :
))
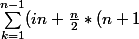Donc on peut dire :
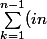 +\sum_{k=1}^{n-1}(\frac{n}{2} * (n+1)))
Vous pouvez me dire si déjà ça c'est juste (pour pas que je continue dans un truc faux mdr) ?
Merci d'avance !
J'ai eu une petite aide de Zermel0 disant qui y'avait un nombre que était constant (Sinon je me barrer a perpet je croyais que les 2 nombre etait constant ...) Donc a partir de la j'ai réussi a avoir :
Donc on peut dire :
Vous pouvez me dire si déjà ça c'est juste (pour pas que je continue dans un truc faux mdr) ?
Merci d'avance !
par chaa13 » 04 Oct 2012, 00:29
Re j'ai essayer de continuer et j'arrive la ça
+\sum_{k=1}^{n-1}(\frac{n}{2}*(n+1))
Pour le
normalement ca marche , mais apres pour l'autre partie je tombe su (n(n+1))/2 qui est la formule de la somme k=1,n et k Y'A pas un truc qui est bizarre ??
Pour le
par zermel0 » 04 Oct 2012, 12:19
non sous les sommes il n'y a pas de k justement, sinon i et j seraient des constantes. Tu as compris à l'envers. Tu dois avoir un i sous la première somme et un j sous la seconde.
par chaa13 » 04 Oct 2012, 14:25
Heu ... La je vois pas trop le but dans 
c'est de le mettre sous forme (n(n+1))/2
par chaa13 » 04 Oct 2012, 18:01
What ? Le fait que ca soit i ou j prouvent le fait que ya une constante ??
par zermel0 » 05 Oct 2012, 11:08
Si tu écris f(x) = a...
a est dans ce cas une constante, ça dépend pas de x.
C'est pareil ici :
si écris "somme de k = 1 à n des a" alors a une constante, et comme tu le sommes n fois, tu auras n*a.
Alors que somme de k=1 à n des k c'est carrément autre chose, k dépend de k (encore heureux) et là c'est notre fameux n(n+1)/2
a est dans ce cas une constante, ça dépend pas de x.
C'est pareil ici :
si écris "somme de k = 1 à n des a" alors a une constante, et comme tu le sommes n fois, tu auras n*a.
Alors que somme de k=1 à n des k c'est carrément autre chose, k dépend de k (encore heureux) et là c'est notre fameux n(n+1)/2
par chaa13 » 05 Oct 2012, 17:16
Donc tu est bien d'accord avec ça maintenant :
}{2})
?
Si c'est juste mdr je viens de me rendre compte que ca change des chose lol ...
Si c'est juste mdr je viens de me rendre compte que ca change des chose lol ...
par zermel0 » 05 Oct 2012, 18:26
C'est exactement ça que tu dois maintenant calculer...
Le terme de droite est facile (ya pas de i ! donc constant)
le terme de gauche, tu peux mettre n devant (factoriser on appelle ça :))
allez vas y :)
Le terme de droite est facile (ya pas de i ! donc constant)
le terme de gauche, tu peux mettre n devant (factoriser on appelle ça :))
allez vas y :)
par chaa13 » 06 Oct 2012, 16:12
Re 
hey !
Bon alors, pour la somme
ca fera : )
Donc on en conclu que
fera : (\frac{i+i(n-1)}{2}))
C'est ca pour cette somme (celle de droite) ?
Merci d'avance !!!!!!!!!!!!!!!!!!
hey !Bon alors, pour la somme
Donc on en conclu que
C'est ca pour cette somme (celle de droite) ?
Merci d'avance !!!!!!!!!!!!!!!!!!
par chaa13 » 06 Oct 2012, 16:43
Mince que je suis bête ! Je me le suis dis y'a 1 heure en y repensant : < surtout n'oublie pas d'inverser le i et le n) mais j'ai oublié p:
Donc ...
Mais la y'aura un probleme on vera pas la différence en n qui est la constante et le n de i a n ??!!
Donc ...
Mais la y'aura un probleme on vera pas la différence en n qui est la constante et le n de i a n ??!!
par Yann64 » 06 Oct 2012, 17:07
zermel0 a écrit:Et dire que parallèlement je lui ai donné un truc le pauvre...
Montrer que pour tout n-uplet de nombres strictements positifs (x1, ... , xn) on a :
(x1 + x2 + ... + xn)(1/x1 + 1/x2 + .... 1/xn) >= n²
Du coup ça, je l'ouvre à tous
Une récurrence, et pour l'hérédité, analyser la fonction x |--> x + 1/x sur R+* en cherchant inf sur R+* de x+1/x.
82 messages
- Page 2 sur 5 - 1, 2, 3, 4, 5
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :