Pour Chaa13
82 messages
- Page 3 sur 5 - 1, 2, 3, 4, 5
zermel0 a écrit:Yann64 --> précise
chaa13 ---> bah on s'en fout que c'est le n issue de la somme avec i, ça doit donner que des trucs avec n à la fin et on s'en fout de leurs origines...
Soit
Montrer que
Récurrence :
Supposons
Supposons que pour
Alors
En utilisant l'hypothèse de récurrence, on a
On cherche à minorer chacun des termes
On cherche en fait la borne inférieure pour
Soit f définie sur
Ce qui signifie que f est décroissante à gauche de 1, et croissante à droite de 1.
La borne inférieure de f est atteinte c'est donc un min, pour x = 1, et f vaut 2 = 1 + 1/1.
En continuant le raisonnement, on aboutit à -------------- >= n^2+1+ 2n = (n+1)^2 CQFD
Désolé pour la fin, c'est long à mettre en forme.
Ce messages est une joke :ptdr:
Vous êtes en train de battre LE record sur Maths-Forum du nombre de messages échangés pour résoudre 3 questions qui peuvent s'expliquer en quelques minutes....
Moi et les miens , nous parions quelques milliers d'Euros ( et je ne m'appelle pas "Nicolas Karabatic" ) que cette discussion va dépasser les 3 pages de messages ?
Merci de me dire si vous acceptez un pari : un chèque de 10.000 euros ? :zen:
a+
ps)
je trouve cela très chouette et dans les faits : il faut prendre ce message comme un compliment pour ce que vous êtes en train de faire/échanger ensemble sur ce forum.....
Vous êtes en train de battre LE record sur Maths-Forum du nombre de messages échangés pour résoudre 3 questions qui peuvent s'expliquer en quelques minutes....
Moi et les miens , nous parions quelques milliers d'Euros ( et je ne m'appelle pas "Nicolas Karabatic" ) que cette discussion va dépasser les 3 pages de messages ?
Merci de me dire si vous acceptez un pari : un chèque de 10.000 euros ? :zen:
a+
ps)
je trouve cela très chouette et dans les faits : il faut prendre ce message comme un compliment pour ce que vous êtes en train de faire/échanger ensemble sur ce forum.....
ptitnoir a écrit:Ce messages est une joke :ptdr:
Vous êtes en train de battre LE record sur Maths-Forum du nombre de messages échangés pour résoudre 3 questions qui peuvent s'expliquer en quelques minutes....
Moi et les miens , nous parions quelques milliers d'Euros ( et je ne m'appelle pas "Nicolas Karabatic" ) que cette discussion va dépasser les 3 pages de messages ?
Merci de me dire si vous acceptez un pari : un chèque de 10.000 euros ? :zen:
a+
ps)
je trouve cela très chouette et dans les faits : il faut prendre ce message comme un compliment pour ce que vous êtes en train de faire/échanger ensemble sur ce forum.....
Ptitnoir, s'il-te-plait, essaie de comprendre que pour un élève de troisième, manipuler des sommes n'est pas toujours évident.
Et puis je lui en ai donné une de niveau maths sup, normal qu'il galère !
Si c'est une joke, je saisis
Edit : j'avais oublié que tu es désormais en seconde Charles ! Bon, ça fait pas trop de différence.
Yann64 a écrit:Soit
Montrer que
Récurrence :
Supposonsle produit vaut
Supposons que pour(\sum_{k=1}^{n}{x_k^{-1}}) \geq n^2)
Alors
En utilisant l'hypothèse de récurrence, on a
On cherche à minorer chacun des termes
On cherche en fait la borne inférieure pourde
Soit f définie surpar
pour
et
Ce qui signifie que f est décroissante à gauche de 1, et croissante à droite de 1.
La borne inférieure de f est atteinte c'est donc un min, pour x = 1, et f vaut 2 = 1 + 1/1.
En continuant le raisonnement, on aboutit à -------------- >= n^2+1+ 2n = (n+1)^2 CQFD
Désolé pour la fin, c'est long à mettre en forme.
Salut !
Oui, c'est faisable avec une récurrence astucieuse, si l'on ne se rate pas dans les calculs
Après je pourrais y arriver en trichant (je me suis aperçu que mon livre apporte une solution détaillée de cet exo), mais je préfère y retoucher quand j'aurai plus de notions en analyse.
Un énoncé niveau Bac+1 serait :
Soit
Calculer
Salut Chaa,
Je vais te montrer la démarche pour aborder un tel calcul.
On va dire que cette somme compte blanc
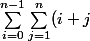\\<br />=\sum_{i=0}^{n-1}\(\sum_{j=1}^n i+\sum_{j=1}^n j\)\\<br />=\sum_{i=0}^{n-1}\(ni+\frac{n(n+1)}{2}\)\\<br />=\sum_{i=0}^{n-1}ni+\sum_{i=0}^{n-1}\frac{n(n+1)}{2}\\<br />=n\sum_{i=0}^{n-1}i+\frac{n^2(n+1)}{2}\\<br />=\frac{n^2(n-1)+n^2(n+1)}{2}\\<br />=n^3)
Si tu ne saisis pas la démarche, n'hésite pas à poser des questions ! Zermel0, Ptitnoir, Yann, moi ou d'autres te répondrons
Je vais te chercher une autre somme similaire à aborder lorsque tu auras parfaitement compris celle-ci ! Et après je retournerai à de l'optique géométrique :dodo:
Je vais te montrer la démarche pour aborder un tel calcul.
On va dire que cette somme compte blanc
Si tu ne saisis pas la démarche, n'hésite pas à poser des questions ! Zermel0, Ptitnoir, Yann, moi ou d'autres te répondrons
Je vais te chercher une autre somme similaire à aborder lorsque tu auras parfaitement compris celle-ci ! Et après je retournerai à de l'optique géométrique :dodo:
ARGHH NNNNNAANn c'est ce que j'ai fait juste qu'a la 4eme ligne, lol ça me dégoûte p: 
Maintenant que je le vois je dis NAAANNN lol j'ai compris le truc ya juste ce moment ou tu met}{2}) =
= }{2}) que je ne comprend pas trop comment tu a fait. Tu peut m'expliquer ?
que je ne comprend pas trop comment tu a fait. Tu peut m'expliquer ?
ARGHH ca me dégoûte !!!
Merci d'avance !!!!!!!!!!!!!!!!
Maintenant que je le vois je dis NAAANNN lol j'ai compris le truc ya juste ce moment ou tu met
ARGHH ca me dégoûte !!!
Merci d'avance !!!!!!!!!!!!!!!!
chaa13 a écrit:ARGHH NNNNNAANn c'est ce que j'ai fait juste qu'a la 4eme ligne, lol ça me dégoûte p:
Maintenant que je le vois je dis NAAANNN lol j'ai compris le truc ya juste ce moment ou tu met=
que je ne comprend pas trop comment tu a fait. Tu peut m'expliquer ?
ARGHH ca me dégoûte !!!
Merci d'avance !!!!!!!!!!!!!!!!
Ah mais c'est bon, n'en fais pas un chichi, tu l'avais presque juste ! J'ose espérer que la prochaine sera la bonne (sinon Batman t'attend au virage !)
Tout simplement parce que la somme
82 messages
- Page 3 sur 5 - 1, 2, 3, 4, 5
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
