Trois losanges pour un hexagone

[Patastronch]

Bon je vois toujours pas le problème mais suite à quelques recherches rapides, il se pourrait que la déformation qu'on fait soit une transformation homographique du plan qui est une transformation bijective. J'ai pas regardé en détail encore, je verrai ça ce soir quand j'aurais plus de temps. Si c'est bien le cas, reste à déterminer la transformation pour s'en assurer.

[Imod]

J'ai bien peur que l'homographie soit complètement définie par l'image du grand hexagone or les pavages sont multiples .

Imod

[Imod]

Une fois établi que chaque pavage correspond à un empilement de cube , le nombre de pavages différents d'un hexagone de côté n ( 1 étant le côté du losange ) est le nombre de matrices , et variant de 1 à n et 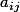de 0 à n , les valeurs 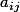étant croissantes sur chaque ligne et sur chaque colonne .

Je ne sais pas si on peut exprimer ce nombre facilement en fonction de n ?

Imod

[scelerat]

Comme Patastronch je ne suis pas du tout convaincu par les arguments de scélérat qui présuppose que le pavage est un empilement de cubes

Desole de revenir si tard, mais je ne suppose pas que c'est un empilement, je le disais pour expliquer.
Changeons donc d'explication : Tarzan ne sait se deplacer que d'un cote de losange au cote parallele. Il part sur un pavage d'un bord du grand hexagone. J'ai donne les arguments qui montrent qu'il arrive au bord oppose en ayant franchi 2n losanges de seulement deux couleurs, et qu'il y arrive a la meme position sur ce bord que celle dont il etait parti. A partir de la, meme Cheetah peut montrer que l'on a n^2 losanges de chaque couleur.

[Imod]

En effet ça marche , je n'avais pas compris ton cheminement ( sûrement à cause de la jungle :hein: ) .

Imod

[Patastronch]

Desole de revenir si tard, mais je ne suppose pas que c'est un empilement, je le disais pour expliquer.
Changeons donc d'explication : Tarzan ne sait se deplacer que d'un cote de losange au cote parallele. Il part sur un pavage d'un bord du grand hexagone. J'ai donne les arguments qui montrent qu'il arrive au bord oppose en ayant franchi 2n losanges de seulement deux couleurs, et qu'il y arrive a la meme position sur ce bord que celle dont il etait parti. A partir de la, meme Cheetah peut montrer que l'on a n^2 losanges de chaque couleur.

Pour ma part il manque la preuve d'existence d'un tel trajet pour chaque point de départ quelque soit le pavage. Bon la démo est assez simple en y réflechissant un peu je te l'accorde.

[Imod]

Le sujet original : Les mathématiques.net

J'ai soumis la solution de scelerat ( j'espère qu'il ne m'en voudra pas ) plus courte que celle de GG ou de ffpower ( en fait assez proche ) . Patastronch reconnaitra sous ma plume l'approche avec déformation de l'hexagone : j'y ai longtemps cru moi-aussi !

Imod

[Patastronch]

En effet c'est exactement la meme méthode que t'avais proposé :cry: Et moi qu'était content d'avoir trouvé une facon de faire originale ...