Détermination de la réciproque d une fonction
49 messages
- Page 1 sur 3 - 1, 2, 3
détermination de la réciproque d une fonction
salut
j aime bien savoir comment déterminer la fonction réciproque dans les deux questions suivantes et justification des étapes de calcul et comment se fait le choix
exercice
1) soit f une fonction définie par f(x)=racine carré( x²+2 x+2) et qui réalise une bijection de IR sur]-1,1[
déterminer l expression de sa fonction réciproque
j ai trouvé deux racines de l équation f(x)=y
x1=-1- (valeur absolue(y))/racine carré(1-y²) et x2=-1+ (valeur absolue(y))/racine carré(1-y²)
2)soit g une fonction définie par g(x)=(x-1)/racine carré( -x²+2 x) et qui réalise une bijection de]0,2[ sur IR
déterminer l expression de sa fonction réciproque
j ai essayé de transformer l équation g(y)=x équivaut (y-1)/racine carré( -y²+2 y)=x comment
suivre et justifier le calcul de l expression de la réciproque
merci
j aime bien savoir comment déterminer la fonction réciproque dans les deux questions suivantes et justification des étapes de calcul et comment se fait le choix
exercice
1) soit f une fonction définie par f(x)=racine carré( x²+2 x+2) et qui réalise une bijection de IR sur]-1,1[
déterminer l expression de sa fonction réciproque
j ai trouvé deux racines de l équation f(x)=y
x1=-1- (valeur absolue(y))/racine carré(1-y²) et x2=-1+ (valeur absolue(y))/racine carré(1-y²)
2)soit g une fonction définie par g(x)=(x-1)/racine carré( -x²+2 x) et qui réalise une bijection de]0,2[ sur IR
déterminer l expression de sa fonction réciproque
j ai essayé de transformer l équation g(y)=x équivaut (y-1)/racine carré( -y²+2 y)=x comment
suivre et justifier le calcul de l expression de la réciproque
merci
Salut !
1) Il y a un problème ; ne réalise certainement pas une bijection de
ne réalise certainement pas une bijection de  vers
vers 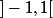 : comment la racine d'un réel (qui devrait être positif) pourrait être négative ?
: comment la racine d'un réel (qui devrait être positif) pourrait être négative ?
1) Il y a un problème ;
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Voici ce que te proposes pour le 2).
On prends dans
dans 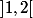 seulement ; justifie qu'alors
seulement ; justifie qu'alors >0) (si ce n'est pas déjà fait).
(si ce n'est pas déjà fait).
Montre qu'alors on peut écrire=\sqrt{-1-\frac{1}{x^2+2x}}) .
.
En posant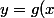) , montre en résolvant l'équation d'inconnue
, montre en résolvant l'équation d'inconnue  et de paramètre
et de paramètre 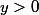 :
:
[CENTER]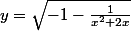 ,[/CENTER]
,[/CENTER]
qu'il y a deux solutions possibles :
[CENTER]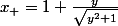 et
et 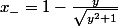 .[/CENTER]
.[/CENTER]
Tu dois savoir que deux fonctions réciproques l'une de l'autre sont symétrique par rapport à la droite d'équation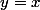 , donc pour savoir laquelle des deux solutions convient, tu peux par exemple raisonner sur la limite en
, donc pour savoir laquelle des deux solutions convient, tu peux par exemple raisonner sur la limite en 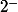 de
de  :
: 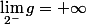 donc on peut raisonnablement penser que si
donc on peut raisonnablement penser que si 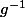 existe, alors
existe, alors 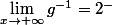 . Cet argument te permettra de conclure sur une partie de la réciproque de
. Cet argument te permettra de conclure sur une partie de la réciproque de 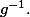 (celle définie sur
(celle définie sur  .
.
Pour celle définie sur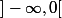 , il suffit de prendre
, il suffit de prendre  dans
dans 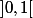
:we:
On prends
Montre qu'alors on peut écrire
En posant
[CENTER]
qu'il y a deux solutions possibles :
[CENTER]
Tu dois savoir que deux fonctions réciproques l'une de l'autre sont symétrique par rapport à la droite d'équation
Pour celle définie sur
:we:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
fautes au niveau des expressions
salut capitaine nuggets
merci pour ta réponse
mais les expressions des deux fonctions sont les suivantes
http://www.casimages.com/i/150704053830739303.png.html
[url][URL=http://www.casimages.com/i/150704053830739303.png.html]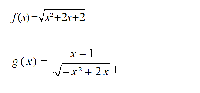 [/url][/URL]
[/url][/URL]
merci
merci pour ta réponse
mais les expressions des deux fonctions sont les suivantes
http://www.casimages.com/i/150704053830739303.png.html
[url][URL=http://www.casimages.com/i/150704053830739303.png.html]
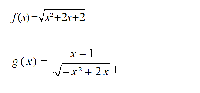 [/url][/URL]
[/url][/URL] merci
plus d explications et expression de la fonction
salut capitaine nuggets]
si possible de m expliquer de plus
Pour celle définie sur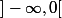 , il suffit de prendre
, il suffit de prendre  dans
dans 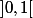
donc la fonctions réciproque est composée de deux morceaux l une sur]0,1[ et l autre ]-1,0[
si possible de me détailler les calculs
merci
si possible de m expliquer de plus
Pour celle définie sur
donc la fonctions réciproque est composée de deux morceaux l une sur]0,1[ et l autre ]-1,0[
si possible de me détailler les calculs
merci
georgets555 a écrit:salut capitaine nuggets]
si possible de m expliquer de plus
Pour celle définie sur, il suffit de prendre
dans
donc la fonctions réciproque est composée de deux morceaux l une sur]0,1[ et l autre ]-1,0[
si possible de me détailler les calculs
merci
la fonctions réciproque est définie sur
Je ne suis pas là pour faire le travail à ta place, il faut que tu fasses les choses par toi-même.
La méthode est quasiment la même :hum:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
autre exemple
salut zygomatique
merci pour ton message
mon problème c est au niveau du choix de la solution
j ai essayé sur l exemple suivant
si possible de me répondre
http://www.casimages.com/i/150704063504331651.png.html
merci
merci pour ton message
mon problème c est au niveau du choix de la solution
j ai essayé sur l exemple suivant
si possible de me répondre
http://www.casimages.com/i/150704063504331651.png.html
merci
merci beaucoup pour votre soutien
salut capitaine nuggets
ne t énerve pas svp
car je n est pas compris votre explication
merci
ne t énerve pas svp
car je n est pas compris votre explication
merci
voir l exemple suivant
salut zygomatique
si possible de me verifier le fichier suivant det de me donner une solution avec plus de détailles
svp pourquoi les valeurs absolues ne servent à rien
voici un autre exemple que j ai essayé de terminer ici les valeurs absolues
http://www.casimages.com/i/150704063504331651.png.html
l
remarque
comment déterminer la valeur a choisir a partir d un tableau de variation de la fonction
merci
si possible de me verifier le fichier suivant det de me donner une solution avec plus de détailles
svp pourquoi les valeurs absolues ne servent à rien
voici un autre exemple que j ai essayé de terminer ici les valeurs absolues
http://www.casimages.com/i/150704063504331651.png.html
l
remarque
comment déterminer la valeur a choisir a partir d un tableau de variation de la fonction
merci
Je ne m'énerve pas du tout :lol3: :we:
Que ne comprends-tu pas dans mon explication ?
Qu'as-tu fait déjà ?
:we:
capitaine nuggets a écrit:Voici ce que te proposes pour le 2).
On prendsdans
seulement ; justifie qu'alors
(si ce n'est pas déjà fait).
Montre qu'alors on peut écrire.
En posant, montre en résolvant l'équation d'inconnue
et de paramètre
:
[CENTER],[/CENTER]
qu'il y a deux solutions possibles :
[CENTER]et
.[/CENTER]
Tu dois savoir que deux fonctions réciproques l'une de l'autre sont symétrique par rapport à la droite d'équation, donc pour savoir laquelle des deux solutions convient, tu peux par exemple raisonner sur la limite en
de
:
donc on peut raisonnablement penser que si
existe, alors
. Cet argument te permettra de conclure sur une partie de la réciproque de
(celle définie sur
.
Pour celle définie sur, il suffit de prendre
dans
:we:
Que ne comprends-tu pas dans mon explication ?
Qu'as-tu fait déjà ?
:we:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
merci beaucoup pour votre soutien
salut capitaine nuggets
merci c est trés gentille
mon problème c est au niveau de l étude de le fonction dans deux intervalles et comment déterminer l expression
donner les expressions sur chaque intervalle car je n est pas compris les deux cas a discuter
(celle définie sur ]0,+\infty[.
Pour celle définie sur ]-\infty,0[, il suffit de prendre x dans ]0,1[)
merci
merci c est trés gentille
mon problème c est au niveau de l étude de le fonction dans deux intervalles et comment déterminer l expression
donner les expressions sur chaque intervalle car je n est pas compris les deux cas a discuter
(celle définie sur ]0,+\infty[.
Pour celle définie sur ]-\infty,0[, il suffit de prendre x dans ]0,1[)
merci
georgets555 a écrit:salut capitaine nuggets
merci c est trés gentille
mon problème c est au niveau de l étude de le fonction dans deux intervalles et comment déterminer l expression
donner les expressions sur chaque intervalle car je n est pas compris les deux cas a discuter
(celle définie sur ]0,+\infty[.
Pour celle définie sur ]-\infty,0[, il suffit de prendre x dans ]0,1[)
merci
De l'expression de
Le problème, c'est que vu que pour
En résumé, on prend
Sinon, pour ta question sur les valeurs absolues, si
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
d autres explication
salut capitaine nuggets
merci pour votre réponse
Donc il faut prendre x dans des différent intervalles ?
1er cas x appartient ]0,1[ donc x-1<0 on prend 1-x>0
2em cas x appartient ]1,2[ donc x-1>0
mais je ne comprend pas comment poursuivre pour avoir le(s) expression(s) de la réciproque
donner moi une réponse avec des détailles pour que je puisse comprendre et finir avec l exercice
merci
merci pour votre réponse
Donc il faut prendre x dans des différent intervalles ?
1er cas x appartient ]0,1[ donc x-1<0 on prend 1-x>0
2em cas x appartient ]1,2[ donc x-1>0
mais je ne comprend pas comment poursuivre pour avoir le(s) expression(s) de la réciproque
donner moi une réponse avec des détailles pour que je puisse comprendre et finir avec l exercice
merci
J't'ai tout mis en te guidant ici :
Commence déjà par suivre les indications que je t'ai donné en essayant de les faire par exemple :lol3:
capitaine nuggets a écrit:Voici ce que te proposes pour le 2).
On prendsdans
seulement ; (...)
Montre qu'alors on peut écrire.
En posant, montre en résolvant l'équation d'inconnue
et de paramètre
:
[CENTER],[/CENTER]
qu'il y a deux solutions possibles :
[CENTER]et
.[/CENTER]
Tu dois savoir que deux fonctions réciproques l'une de l'autre sont symétrique par rapport à la droite d'équation, donc pour savoir laquelle des deux solutions convient, tu peux par exemple raisonner sur la limite en
de
:
donc on peut raisonnablement penser que si
existe, alors
. Cet argument te permettra de conclure sur une partie de la réciproque de
(celle définie sur
.
Pour celle définie sur, il suffit de prendre
dans
:we:
Commence déjà par suivre les indications que je t'ai donné en essayant de les faire par exemple :lol3:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
il n'est pas nécessaire de tout mettre sous une racine ...
par contre x(2 - x) changeant de sens de variation en 1 il est effectivement nécessaire (probablement) de distinguer x < 1 de x > 1 ... pour avoir la bijectivité .... qui sera connue par l'étude des variations ...
par contre x(2 - x) changeant de sens de variation en 1 il est effectivement nécessaire (probablement) de distinguer x < 1 de x > 1 ... pour avoir la bijectivité .... qui sera connue par l'étude des variations ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
comment exploiter le tableau de variation
salut zygomatique
juste une question comment écrire avec le latex car je le maîtrise pas (aucune idée ) ( les logiciels qu il faut installer et la création des PDF ), comment faire un tableau de variation, des courbes de fonctions et des figures géométriques 2D et 3D etc)
a propos de notre exercice
svp représenter moi le tableau de variation
l'étude des variations de qu elle fonction exactement
car j aime savoir comment l exploiter pour déterminer la fonction réciproque
merci
juste une question comment écrire avec le latex car je le maîtrise pas (aucune idée ) ( les logiciels qu il faut installer et la création des PDF ), comment faire un tableau de variation, des courbes de fonctions et des figures géométriques 2D et 3D etc)
a propos de notre exercice
svp représenter moi le tableau de variation
l'étude des variations de qu elle fonction exactement
car j aime savoir comment l exploiter pour déterminer la fonction réciproque
merci
49 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
