Je regarde aussi.
Mais je préfère une liste d'équation à une figure paint.
La vérification est plus facile.
3 cercles tangent à un 4ème
27 messages
- Page 2 sur 2 - 1, 2
En fait, je reproche à ta figure de ne pas respecter les dimensions que j'ai données.
Je n'ai pas prétendu que si les centres sont alignés, alors il n'y a pas huit cercles tangents.
J'ai juste dit qu'il n'y a pas toujours huit cercles.
J'ai modifié mon message précédent pour rendre les choses plus évidentes.
Je n'ai pas prétendu que si les centres sont alignés, alors il n'y a pas huit cercles tangents.
J'ai juste dit qu'il n'y a pas toujours huit cercles.
J'ai modifié mon message précédent pour rendre les choses plus évidentes.
Les équations, c'est ça :
^2+y^2=(R\pm 1.9)^2)
^2)
^2+y^2=(R\pm 1.8)^2)
La 2em équation donne^2-x^2)
La première donne ensuite^2-(R\pm 2)^2-25))
et il nous reste^2+(R\pm 1.8)^2-2(R\pm 2)^2) dont les solution sont :
dont les solution sont :
avec --- : R=85.5 ; x=-0.829 ; : 2 solutions
: 2 solutions
avec --+ : R=-3.32 : pas de solutions
avec -+- : R=6.55769 ; x=-2.4078 ; : 2 solutions
: 2 solutions
avec -++ : R=-6.23 : pas de solutions
Et comme j'en ait marre, je te laisse les 4 derniers cas (+-- ; +-+ ; ++- ; +++) et vérifier qu'au total, il y a bel et bien 8 solutions.
P.S. Et je persiste à penser que, si on compte les éventuelles droites comme solutions, il y a toujours 8 solutions lorsque les 3 disques fermés sont disjoints.
Je vais réfléchir à la preuve la plus simple (et surtout la moins calculatoire) que l'on puisse produire...
La 2em équation donne
La première donne ensuite
et il nous reste
avec --- : R=85.5 ; x=-0.829 ;
avec --+ : R=-3.32 : pas de solutions
avec -+- : R=6.55769 ; x=-2.4078 ;
avec -++ : R=-6.23 : pas de solutions
Et comme j'en ait marre, je te laisse les 4 derniers cas (+-- ; +-+ ; ++- ; +++) et vérifier qu'au total, il y a bel et bien 8 solutions.
P.S. Et je persiste à penser que, si on compte les éventuelles droites comme solutions, il y a toujours 8 solutions lorsque les 3 disques fermés sont disjoints.
Je vais réfléchir à la preuve la plus simple (et surtout la moins calculatoire) que l'on puisse produire...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut
Avec geogebra, ça donne ça:
"A la règle et au compas", ce serait pour le moins laborieux.
Ah, le compas ! Il fallait chercher un trou dans le tableau noir pour y insérer sa pointe métallique. Au besoin, on faisait le trou en donnant un coup de pointe ... Certains profs préféraient une ficelle ...
Catastrophe lorsque les tableaux blancs sont arrivés; on a vu des compas avec des ventouses qui ne permettaient pas de visualiser le centre.
Bon, mais sans compas, électronique ou "réel", pas de géométrie.
Avec geogebra, ça donne ça:

"A la règle et au compas", ce serait pour le moins laborieux.
Ah, le compas ! Il fallait chercher un trou dans le tableau noir pour y insérer sa pointe métallique. Au besoin, on faisait le trou en donnant un coup de pointe ... Certains profs préféraient une ficelle ...
Catastrophe lorsque les tableaux blancs sont arrivés; on a vu des compas avec des ventouses qui ne permettaient pas de visualiser le centre.
Bon, mais sans compas, électronique ou "réel", pas de géométrie.
Je trouve pas de jolie méthode sans trop de calcul (alors que je suis à peu prés sûr qu'il y en a au moins une : ceux qui veulent chercher...)
Par le calcul, on peut quand même simplifier le problème. On prend d'abord une inversion centré sur un point I d'un des cercles Co pour transformer ce cercle en droite. Les deux autres cercles restent des cercles et sont situés du même coté de la droite vu qu'ils étaient tout les deux à l'extérieur du cercle qui est devenu une droite.
On prend la droite en question comme axe des x et, quitte à faire une homothétie, on peut supposer que les 2 cercles restants sont centrés en (1,a) et (-1,b) avec a,b>0 et de rayon respectifs et
et  .
.
Les disques fermés étant disjoint (et les cercles supposés non réduit à des points), on a :
 [TEX]y=r) (le cercle est tangent à l'axe des x et du même coté que les deux autres)
(le cercle est tangent à l'axe des x et du même coté que les deux autres)
(2)^2+(y-a)^2=(r+\epsilon \alpha)^2\) où
où 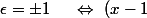^2=(a+\epsilon \alpha)(2r -a+\epsilon\alpha)=:A(2r-A'))
(3)^2+(y-b)^2=(r+\delta \beta )^2\) où
où 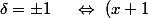^2=(b+\delta \beta)(2r -b + \delta\beta)=:B(2r-B'))
(3)-(2) donne et il reste à résoudre (par exemple) (3) :
et il reste à résoudre (par exemple) (3) :
^2=B(2r-B')\ \ \ \ \) qui, une fois simplifiée donne :
qui, une fois simplifiée donne :
^2r^2-\big((B-A)(BB'-AA')+4(A+B)\big)r +\frac{(AA'-BB')^2}{4}+2(AA'+BB')+4=0)
 Si
Si 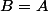 alors l'équation n'est que du premier degré. Elle admet une unique solution
alors l'équation n'est que du premier degré. Elle admet une unique solution  qui est clairement
qui est clairement 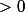 . Mais le fait que
. Mais le fait que 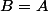 signifie que la droite d'équation
signifie que la droite d'équation 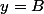 est tangente aux deux cercles et, une fois qu'on aura refait l'inversion de centre I pour retransformer l'axe des x en Co, cette droite deviendra un cercle (ou une droite) tangente à Co en I. Donc dans ce cas, l'équation produit bien DEUX solutions.
est tangente aux deux cercles et, une fois qu'on aura refait l'inversion de centre I pour retransformer l'axe des x en Co, cette droite deviendra un cercle (ou une droite) tangente à Co en I. Donc dans ce cas, l'équation produit bien DEUX solutions.
 Si
Si  , on a affaire à une équation du second degré de discriminant
, on a affaire à une équation du second degré de discriminant
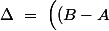(BB'-AA')+4(A+B)\Big)^2-(B-A)^2\Big((AA'-BB')^2+8(AA'+BB')+16\Big)=\cdots)
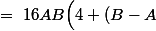(B'-A')\Big)\ =\ 16AB\Big(4+(b-a)^2-(\delta\beta-\epsilon\alpha)^2\Big)\ >\ 0)
L'équation admet donc deux solutions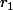 et
et 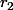 de même signe vu que
de même signe vu que
^2+8(AA'+BB')+16}{4(B-A)^2}\ >\ 0)
et ce signe est positif car :
(BB'-AA')+4(A+B)}{(B-A)^2}\ =\ \frac{B\big(4+(B-A)(B'+A')\big)+(B-A)^2A'+4A)}{(B-A)^2}\ >\ 0)
Conclusion : chacune des 4 équations du second degrés (selon que l'on prend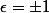 ;
;  ) produit deux solutions distinctes et ces 8 solutions sont distinctes vu que le choix, par exemple, de
) produit deux solutions distinctes et ces 8 solutions sont distinctes vu que le choix, par exemple, de 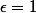 correspond à chercher des cercle tangent extérieurement à celui de centre (1,a) et celui de
correspond à chercher des cercle tangent extérieurement à celui de centre (1,a) et celui de 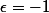 corespond à chercher des cercle tangents ET contenant celui de centre (1,a).
corespond à chercher des cercle tangents ET contenant celui de centre (1,a).
Donc, il y a bel et bien toujours 8 solutions et... aucun cas particuliers... (à part évidement celui où une/des droites qui sont tangentes aux 3 cercles et qu'on doit compter parmi les 8 solutions)
Par le calcul, on peut quand même simplifier le problème. On prend d'abord une inversion centré sur un point I d'un des cercles Co pour transformer ce cercle en droite. Les deux autres cercles restent des cercles et sont situés du même coté de la droite vu qu'ils étaient tout les deux à l'extérieur du cercle qui est devenu une droite.
On prend la droite en question comme axe des x et, quitte à faire une homothétie, on peut supposer que les 2 cercles restants sont centrés en (1,a) et (-1,b) avec a,b>0 et de rayon respectifs
Les disques fermés étant disjoint (et les cercles supposés non réduit à des points), on a :
(2)
(3)
(3)-(2) donne
L'équation admet donc deux solutions
et ce signe est positif car :
Conclusion : chacune des 4 équations du second degrés (selon que l'on prend
Donc, il y a bel et bien toujours 8 solutions et... aucun cas particuliers... (à part évidement celui où une/des droites qui sont tangentes aux 3 cercles et qu'on doit compter parmi les 8 solutions)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
27 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

