Factorielles

[theluckyluke]

Salut,

Pour la démo par récurrence, il faut procéder comme ceci :

Notons la proposition ""

Initialisation : donne et donc on a bien

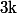
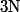
Hérédité : Supposons vraie, et montrons par récurrence pour tout dans privé de .

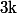
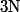
Soit dans privé de .
Comme est vraie, on a
On a donc et donc

On a donc car pour

Donc est vraie.
On en déduit donc que est vraie.

Thomas G :zen:

juste un truc, pourrait-on faire :

Notons la proposition ""

Initialisation : donne et donc on a bien

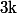
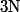
Hérédité : Supposons vraie, et montrons par récurrence pour tout dans privé de .

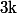
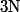
Soit dans privé de .
Comme est vraie, on a


On a donc qui équivaut à et ceci est vrai car pour

Donc est vraie.
On en déduit donc que est vraie.


Quelle est la différence entre les deux?

[nekros]

Salut,

Non car il faut montrer que

Thomas G :zen:

[theluckyluke]

Salut,

Non car il faut montrer que

Thomas G :zen:

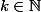
pourtant la question est bien:démontrer par récurrence que pour tout *, on a :
donc pourquoi ça ne va pas si on prouve que ???

[nekros]

Tu es d'accord que est la proposition :
Donc est la proposition

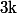
Il suffit de remplacer par .

Thomas G :zen:

[theluckyluke]

Tu es d'accord que est la proposition :
Donc est la proposition

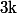
Il suffit de remplacer par .

Thomas G :zen:

ah ouais! ok, j'ai pas pensé qu'il fallait remplacer aussi de l'autre côté de l'inégalité.

merci!

[nekros]

De rien :we:

Thomas G :zen:

[olivthill]

Je me demande ce que donne U de zéro.
Il a été dit que U0 égal à 0.
Pourtant factoriel de zéro est égal à un, et 1/1=1.

[nekros]

salut,

Tu parles de quelle suite ? :hein:

Thomas G :zen:

[olivthill]

Je parle de la suite Un du message initial. C'est vrai que c'était il y a très longtemps, puisque c'était hier.

Pour n = 0, est-ce que cela fait ?

[nekros]

oui :++: 0!=1 par convention

Thomas G :zen:

PS : C'est vrai que c'était il y a très longtemps, puisque c'était hier

Ironie ? :ptdr:

[said_271]

k!>ou= 2êxp(k-1)
pour k=1 : 1!=1 et 2exp(1-1)=1 donc cé vrai
suposons quecé vrai a l'ordre n et montrons pour n+1
(n+1)!=n!x(n+1)>ou =2exp(n-1)(n+1)
et n+1>=2 donc (n+1)!>= 2exp(n-1)x2=2expn
ce qu'il falait démontrer
Un=somme de 0 a n des (k!)exp(-1)
U0=(0!)exp(-1)=1
U1=(0!)exp(-1)+(1!)exp(-1)=1+1=2
U2=1/0! +1/1! +1/2! =1+1+1/2=5/2
U3=1/0! +1/1! +1/2! +1/3! =1+1+1/2+1/6=16/6
pour la croissance de la suite
U(n+1)-Un=1/(n+1)! >0 donc U(n+1)>Un alors c'est une suite croissante

[aviateurpilot]

je pense que le probeme a ete resoulu

vous cherchez maintenant la limite de ??

[said_271]

limite de Un
k!>=2exp(k-1) donc 1/k!=<1/2exp(k-1)
donc Un=<1+somme de 1 a ndes 1/2exp(k-1) =1+(1/(2expn ) -1)/1/2 -1
c'est suite geométrique de raison 1/2
donc par passage a la limite
un<=1+2=3 donc la limite Un est <=3

[aviateurpilot]

je confirme

donc

[aviateurpilot]

pour que la limite soit 3

il faut montrer qu'il existe tel que quelque

[said_271]

la limite de ta suite ni autre e=2.71........
si tu fais un devellopemen limité de la fonction exponentielle
e expx = somme de 0 a l'infinie des xexpn/n!
et si tu donne a x la valeur tu va voir e= limite a l'infini de Un

[aviateurpilot]

je ne connais pas

un devellopemen limité

:hein: :hein:

[nekros]

De quelle suite parler vous ??

Thomas G :zen:

[said_271]

l'enencé de ton probleme te permette seulement d'encadrer la limite l de te suite entre 16/5=U3 et 3donc16/5<= l<=3 puisque ta suite est croissante
pour t'aprocher de la limite tu n'a qu'a calculer d'autre terme de la suite de plus en plus grand