Applications de IR² dans IR

[Luc]

j'en déduis alors que :

Ok. Tu y es presque maintenant. Pense à utiliser que

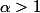
[capitaine nuggets]

Ok. Tu y es presque maintenant. Pense à utiliser que

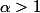
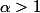
donc mais je ne vois pas à quoi ça m'avance...

[Luc]

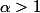
donc mais je ne vois pas à quoi ça m'avance...

Il y a de l'idée mais là tu perds de l'information.

Tu sais majorer normalement.

[capitaine nuggets]

Il y a de l'idée mais là tu perds de l'information.

Tu sais majorer normalement.

Alors :

[Luc]

Alors :

Majorer par une constante qui ne dépend pas de x et y.

[capitaine nuggets]

Il y a de l'idée mais là tu perds de l'information.

Tu sais majorer normalement.

Ou alors :

[capitaine nuggets]

Il y a de l'idée mais là tu perds de l'information.

Tu sais majorer normalement.

Ou alors :



Donc :
et donc .

Ou alors je dois dire que pour toutes suites de réelles et : en .

[Luc]

Ou alors :

Oui!
Là tu as presque fini.

[capitaine nuggets]

Alors :
et donc .

Ou alors je dois dire que pour toutes suites de réelles et : en

[capitaine nuggets]

Alors :
et donc .

Ou alors je dois dire que pour toutes suites de réelles et : en

[capitaine nuggets]

si tu es d'accord avec moi j'aimerais traité un autre exemple :
Je considère la fonction pour et .

est clairement définie pour tous réels .
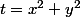
Je pose et donc je montre que donc est continue.
Ai-je bon ?

[Luc]

Alors :
et donc .

Oui mais tu as oublié la valeur absolue, et il faut justifier que tend vers 0 (c'est vrai car ).

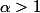
EDIT : bizzare, j'arrive à citer tes posts mais ma réponse s'affiche avant ton post!

[capitaine nuggets]

Si tu es d'accord avec moi j'aimerais traité un autre exemple :
Je considère la fonction pour et .

est clairement définie pour tous réels .
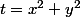
Je pose et donc je montre que donc est continue.
Ai-je bon ?

[capitaine nuggets]

Si tu es d'accord avec moi j'aimerais traité un autre exemple :
Je considère la fonction pour et .

est clairement définie pour tous réels .
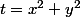
Je pose et donc je montre que donc est continue.
Ai-je bon ?

Oui mais tu as oublié la valeur absolue, et il faut justifier que tend vers 0 (c'est vrai car ).

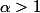
EDIT : bizzare, j'arrive à citer tes posts mais ma réponse s'affiche avant ton post!

j'ai replacer mon post pour réunir mes deux derniers posts en un !

[Luc]

Oui, c'est pas mal, sauf que c'est t^(2/3) et pas t^(3/2).
Comment montres-tu que t^(2/3)arctan(1/t) tend vers 0?

Sinon, tu peux remarquer directement que arctan est une fonction bornée, et cela montre le résultat (et même un peu mieux).

[capitaine nuggets]

Oui, c'est pas mal, sauf que c'est t^(2/3) et pas t^(3/2).
Comment montres-tu que t^(2/3)arctan(1/t) tend vers 0?

Sinon, tu peux remarquer directement que arctan est une fonction bornée, et cela montre le résultat (et même un peu mieux).

oui, j'ai fait une erreur c'est 3/2 l'exposant.
ben en montrant que donc d'où la limite nulle.
Ok ?

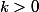
Sinon, si on a une fonction où et qu'on suppose qu'il existe un réel , tel que : (je crois qu'on dit que est -lipschitzienne). Comment montrer que est continue sur ?

[Luc]

oui, j'ai fait une erreur c'est 3/2 l'exposant.
ben en montrant que donc d'où la limite nulle.
Ok ?

Ok.

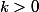
Sinon, si on a une fonction où et qu'on suppose qu'il existe un réel , tel que : (je crois qu'on dit que est -lipschitzienne). Comment montrer que est continue sur ?

En revenant à la définition de la continuité avec des .

[capitaine nuggets]

Ok.

En revenant à la définition de la continuité avec des .

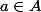
soit . est continue en si et seulement si , implique .

Mais comment exploiter la définition ?

[Luc]

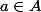
soit . est continue en si et seulement si , implique .

Mais comment exploiter la définition ?

Tu définis un fixé et tu cherches un qui convient.

[capitaine nuggets]

Tu définis un fixé et tu cherches un qui convient.

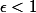
J'hésité entre et ?