Fermé de IR²
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 04 Jan 2008, 01:31
par legeniedesalpages » 04 Jan 2008, 01:31
Bonsoir,
je ne vois pas comment montrer que
\in \mathbb{R}^2:\ y\leq x\})
.
Merci pour votre aide.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 04 Jan 2008, 01:37
par tize » 04 Jan 2008, 01:37
Salut,
\in \mathbb{R}^2:\ y\leq x\}=f^{-1}\([0;+\infty[\))
avec
=x-y)
continue de

dans

 par legeniedesalpages » 04 Jan 2008, 01:37
par legeniedesalpages » 04 Jan 2008, 01:37
Est-ce que je peux par exemple utiliser la caractérisation séquentielle de l'adhérence de cette façon:
Soit
)
une suite de points de
\in \mathbb{R}^2:\ y\leq x\})
convergeant vers un point
 \in \mathbb{R}^2)
.
on a alors

et

et pour tout

, on a

.
En passant à la limite, on a alors
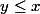
.
Donc
\in \mathbb{R}^2:\ y\leq x\})
est fermé.
 par legeniedesalpages » 04 Jan 2008, 01:38
par legeniedesalpages » 04 Jan 2008, 01:38
tize a écrit:Salut,
\in \mathbb{R}^2:\ y\leq x\}=f^{-1}\([0;+\infty[\))
avec
=x-y)
continue de

dans

ah oui c'est vrai, :mur: merci Tize.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 04 Jan 2008, 01:39
par tize » 04 Jan 2008, 01:39
legeniedesalpages a écrit:Est-ce que je peux par exemple utiliser la caractérisation séquentielle ...
Oui pourquoi pas... :we:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 04 Jan 2008, 01:45
par ThSQ » 04 Jan 2008, 01:45
... est fermé j'imagine ;)
Avec une fonction C° :
f : IR² -> R f(x,y) = x-y est C°
ton truc = f^{-1}([0,+oo[) image réciproque d'un fermé
Ou des suites :
Si (x(n),y(n)) truc² -> (x,y) E R² on a x(n) >= y(n) donc x >= y et (x,y) truc²
Ou des ouverts
Si x
Edit : grillé par tize
 par legeniedesalpages » 04 Jan 2008, 01:59
par legeniedesalpages » 04 Jan 2008, 01:59
ah oui par les ouverts j'y avais pas pensé.
 par legeniedesalpages » 04 Jan 2008, 02:12
par legeniedesalpages » 04 Jan 2008, 02:12
est-ce que les fonctions polynômiales à plusieurs variables sont encore continues dans IR ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 04 Jan 2008, 02:14
par tize » 04 Jan 2008, 02:14
oui...qu'entends tu par "encore"
 par legeniedesalpages » 04 Jan 2008, 02:15
par legeniedesalpages » 04 Jan 2008, 02:15
tize a écrit:oui...qu'entends tu par "encore"
je connaissais seulement le résultat sur IR avec une seule variable.
 par legeniedesalpages » 04 Jan 2008, 02:21
par legeniedesalpages » 04 Jan 2008, 02:21
en fait je dois justifier dans

de

avec
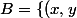\in \mathbb{R}^2:\ x \geq 1 \mbox{ et } 1\leq y \leq x\})
et
= :=\frac{1}{x^2y})
.
Je pensais commencer par voir si g est continue afin de voir si elle est mesurable.
 par legeniedesalpages » 04 Jan 2008, 02:30
par legeniedesalpages » 04 Jan 2008, 02:30
legeniedesalpages a écrit:en fait je dois justifier dans

de

avec
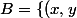\in \mathbb{R}^2:\ x \geq 1 \mbox{ et } 1\leq y \leq x\})
et
= :=\frac{1}{x^2y})
.
Je pensais commencer par voir si g est continue afin de voir si elle est mesurable.
En fait je crois que c'est bon,
je dis simplement que g est continue donc mesurable, de plus
\leq 1,)
quelque soit
\in \mathbb{R}^2)
.
Donc

, et

qui a pour mesure

.

étant positive,

existe dans

.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 04 Jan 2008, 11:13
par ThSQ » 04 Jan 2008, 11:13
legeniedesalpages a écrit:\leq 1,)
quelque soit
\in \mathbb{R}^2)
.
J'ai pas tout lu mais ça me paraît louche ça
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 04 Jan 2008, 12:17
par tize » 04 Jan 2008, 12:17
Legénie a peut être voulu écrire
\in B)
...
 par legeniedesalpages » 04 Jan 2008, 13:48
par legeniedesalpages » 04 Jan 2008, 13:48
legeniedesalpages a écrit:en fait je dois justifier dans

de

avec
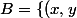\in \mathbb{R}^2:\ x \geq 1 \mbox{ et } 1\leq y \leq x\})
et
= :\frac{1}{x^2y})
.
Je pensais commencer par voir si g est continue afin de voir si elle est mesurable.
Je ne vois pas comment intégrer cette fonction g sur B, même en utilisant Fubini, ce qui me gêne c'est déterminer les bornes de l'intégrale de y, qui vairent.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 04 Jan 2008, 14:18
par ThSQ » 04 Jan 2008, 14:18
legeniedesalpages a écrit:oui pardon, je voulais dire dans B.
Oui c'était clair en fait, j'aurais dû tout lire ... :marteau: :briques:
Sinon pour ton intégrale, peut-on faire comme ça ? (je sais pas si c'est légal, j'ai pas vu les intégrales multiples encore ...)
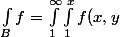 = \int _1^\infty dx/x^2 \times \int_1^x 1dy/y)
+ primitive ln(x)/x² = - (ln(x)+1)/x
 par legeniedesalpages » 04 Jan 2008, 14:35
par legeniedesalpages » 04 Jan 2008, 14:35
ThSQ a écrit:Oui c'était clair en fait, j'aurais dû tout lire ... :marteau: :briques:
Sinon pour ton intégrale, peut-on faire comme ça ? (je sais pas si c'est légal, j'ai pas vu les intégrales multiples encore ...)
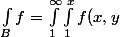 = \int _1^\infty dx/x^2 \times \int_1^x 1dy/y)
+ primitive ln(x)/x² = - (ln(x)+1)/x
Il faut le justifier je pense à l'aide du théorème de Fubini, qu'on a bien:
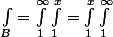
 par legeniedesalpages » 04 Jan 2008, 14:55
par legeniedesalpages » 04 Jan 2008, 14:55
ok dans le cours j'ai ce résultat (fubini quand on intègre sur un ensemble mesurable

de

):
si

est
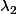
intégrable sur

(qui est
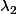
-mesurable), on a:
 d(x,y) =\qquad \bigint_{Proj_{\mathbb{R}}^{(y)}(B)}\ \ (\bigint_{B^y} f(x,y) dx) dy =\qquad \bigint_{Proj_{\mathbb{R}}^{(x)}(B)}\ \ (\bigint_{B^x} f(x,y) dy) dx)
,
avec
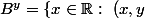\in B\})
,
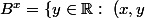\in B\})
,
}(B) = \{v\in \mathbb{R}:\ \exists u \in \mathbb{R},\ (u,v)\in B\})
,
}(B) = \{u\in \mathbb{R}:\ \exists v \in \mathbb{R},\ (u,v)\in B\})
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
de
avec
et
.
de
avec
et
.