fatal_error a écrit:de manière officielle cette fois.(...)
Je n'ai pas lu tous les messages de la discussion, vous imaginez pourquoi.
Mais comme dlzlogic m'a contacté par MP en me posant la question, malgré tout, je vais essayé encore une fois de clarifier la situation sur un exemple simple. Je vois que pas mal de gens ont déjà fait le boulot, tant pis si je ne fais que répéter, quitte à perdre mon temps :lol3:
Première expérience : 10^3 lancés de dé
histogramme observé (respectivement aux numéros des faces du dé) : [157, 154, 166, 189, 173, 161]
espérance observée = 3.55
écart-type observé = 1.676156317
En conservant évidemment ces deux caractéristiques pour la loi normale, on compare la distribution observée (en bleu), celle uniforme (en noir), et la normale (en rouge) :

On voit clairement que l'observation colle avec la loi uniforme et pas la loi normale !
Seconde expérience : 10^4 lancés de dé
histogramme observé : [1733, 1643, 1691, 1639, 1610, 1684]
espérance observée = 3.4802
écart-type observé = 1.717675161
En conservant évidemment ces deux caractéristiques pour la loi normale, on compare la distribution observée (en bleu), celle uniforme (en noir), et la normale (en rouge) :

On voit clairement que l'observation colle avec la loi uniforme et pas la loi normale !
Pour mémoire, pour un dé non pipé, on a en théorie :
espérance = 3.5
écart-type = 1.707825129
Dans l'expérience de n=10^3 lancés de dé, la répartition observée est [157, 154, 166, 189, 173, 161].
Dans l'expérience de n=10^4 lancés de dé, la répartition observée est [1733, 1643, 1691, 1639, 1610, 1684].
Ces expériences confirment une équiprobabilité des faces du dé avec p=1/6.
Mais voilà ce que Dlzlogic évoquait (chacun constatera et comprendra pourquoi il ne le fait pas clairement).
On peut voir chacune des deux expériences (montrant la loi uniforme sur l'ensemble des faces) comme 6 expériences de Bernouilli, illustrant la
loi binomiale (qui s'approxime classiquement par la
loi normale, voir wikipédia par exemple). Précisément, il s'agit de la loi
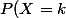 = {n \choose k} p^k (1-p)^{n-k})
avec p=1/6 et n=10^3 ou n=10^4
(ou si on préfère la loi normale d'espérance np et d'écart type
})
, voir wikipédia par exemple).
En ce qui concerne la première expérience avec n=10^3, l'intervalle I = [155,178] doit théoriquement contenir environ 69% des valeurs de l'histogramme [157, 154, 166, 189, 173, 161] (d'ailleurs, on voit qu'il en contient 4/6, ce qui est conforme à la théorie). Pourquoi cet intervalle I ? J'ai arbitrairement pris " l'espérance plus ou moins l'écart-type "
})
. Pourquoi 69% ? Car
 = 0.6915...)
En ce qui concerne la seconde expérience avec n=10^4, l'intervalle I = [1629, 1704] doit théoriquement contenir environ 69% des valeurs de l'histogramme [1733, 1643, 1691, 1639, 1610, 1684] (d'ailleurs, on voit qu'il en contient 4/6 encore une fois). Again : pourquoi cet intervalle I ? J'ai arbitrairement pris " l'espérance plus ou moins l'écart-type "
})
. Pourquoi 69% ? Car
 = 0.6921...)
Dans la pratique, on prend souvent un autre intervalle "plus sûr" (à 95%, et non 69%)
})
, mais je n'ai pas fait ce choix ici pour montrer qu'on peut sortir de l'intervalle théorique, 69% étant largement inférieur à 100% ! Baf...
Voilà, c'est l'illustration parfaite de la
loi binomiale avec p=1/6 (ou la
loi normale si on fait l'approximation habituelle) d'une expérience de Bernouilli ...qui est valide parce que
loi uniforme sur les faces du dé avec p=1/6. CQFD ? :lol3:
Et tout ceci est expliqué clairement dans les manuels de stat/proba de lycée (en seconde ou terminale), il n'y a aucun secret, aucun miracle.


