Loi uniforme
13 messages
- Page 1 sur 1
loi uniforme
salut
Soit X une variable aléatoire de loi uniforme sur [-2,3]
1.Calculer P( X==1)
si jai bien capté c'est la proba de X==1
c'est donc la proba de X==1)
si quelqu'un avait une petite explication ça serait génial
Soit X une variable aléatoire de loi uniforme sur [-2,3]
1.Calculer P( X==1)
si jai bien capté c'est la proba de X==1
c'est donc la proba de X==1)
si quelqu'un avait une petite explication ça serait génial
Oui, lors de probabilité conditionnelle il faut toujours partir de la définition. Ici dans ton cas on a :

Tu ramène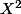 en
en  et tu calcules (je te laisse le soin de le faire, car c'est trivial)...
et tu calcules (je te laisse le soin de le faire, car c'est trivial)...
Pour la fonction de répartition c'est bien ça, sauf que ça doit dépendre obligatoirement d'un paramètre. Ici tu as par exemple, pour tout :
:
 = P[X < t] = \int_{-\infty}^{t}\frac{1}{(3-2)}I_{[-2.3](x)dx})
et donc tu es obligé de différencier plusieurs cas :
Premierement, si alors
alors  = 0) .
.
Deuxièmement, si alors :
alors :
 = \int_{-\infty}^{t}\frac{1}{(3-2)}I_{[-2.3](x)dx} = \int_{-2}^{t}dx = t-2) .
.
Enfin, si alors :
alors :
 = \int_{-2}^{3}xdx = 3-2 = 1)
Par conséquent, pour tout il vient :
il vient :
 = \left \lbrace<br /> \begin{array}{c}<br /> 0 \,\,\textrm{si}\,\, t \leq -2<br /> \\<br /> t-2 \,\,\textrm{si}\,\, t \in [-2,3]<br />\\<br />\\<br />1 \,\,\textrm{si}\,\, t \geq 3<br /> \end{array}<br /> \right.)
Je te laisse faire ce même raisonnement pour la densité de probabilité de la variable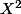 .
.
Tu ramène
Pour la fonction de répartition c'est bien ça, sauf que ça doit dépendre obligatoirement d'un paramètre. Ici tu as par exemple, pour tout
et donc tu es obligé de différencier plusieurs cas :
Premierement, si
Deuxièmement, si
Enfin, si
Par conséquent, pour tout
Je te laisse faire ce même raisonnement pour la densité de probabilité de la variable
Pas du tout, la loi de la v.a  n'est pas du tout une loi uniforme (malheureusement, sinon ton exo serai trop "facile" :zen:)...
n'est pas du tout une loi uniforme (malheureusement, sinon ton exo serai trop "facile" :zen:)...
Pour une piste regarde un peu ici :
carré d'une loi uniforme
Pour une piste regarde un peu ici :
carré d'une loi uniforme
Nous sommes dans ton exercice dans le cas d'une loi continue, par conséquent la définition de la fonction de répartition  de la v.a
de la v.a  possèdant une densié de probabilité f est pour tout
possèdant une densié de probabilité f est pour tout  :
:
 := \int_{-\infty}^{t} f(x)dx)
Maintenant, particulièrement pour une loi uniforme ta formule est effectivement vérifiée...mais attention ce n'est pas la définition de la fonction de répartition générale, ta formule serai plutôt une propriété des lois uniformes.
P.S : rattrapages ?
Maintenant, particulièrement pour une loi uniforme ta formule est effectivement vérifiée...mais attention ce n'est pas la définition de la fonction de répartition générale, ta formule serai plutôt une propriété des lois uniformes.
P.S : rattrapages ?
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 98 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
