Dlzlogic a écrit: Citation:
Posté par fatal_error
Es-tu d'accord qu'en tracant la courbe qui au numero de face du de associe le nombre de fois que le de est sorti que on a a peu pres une droite horizontale? (et donc pas une gaussienne?) [fin de citation]
Oui, ce qui signifie, en d'autres termes que le dé se souvient du nombre de fois que chaque face est sortie.
Avec ces citations imbriquées je sais pas très bien qui a dit quoi dans le texte ci-dessus, mais quoi qu'il en soit il est absolument faux de dire que le dé se souvient du nombre de fois que chaque face est sortie. Si je pose un dé normal sur une table devant toi, il n'y a aucun moyen d'accéder à l'histoire des tirages de ce dé. Dire que les tirages de dé respectent une loi uniforme n'est en aucune façon équivalent à dire que le dé fait un effort pour la respecter la loi uniforme ou que le dé se souvient de ce qu'il a sorti précédemment et agit en conséquence.
Dire que le dé se souvient de ce qu'il a sorti précédemment (et il se souvient à partir de quand, d'ailleurs ?) c'est dire ce que Dlzlogic a déjà dit de nombreuses fois, à savoir que si un dé équilibré sort 1000 fois de suite la face 6 (événement très rare mais pas impossible) alors il a une probabilité quasi-nulle de sortir 6 au 1001ème tirage. Cela est faux, profondément faux et les simulations avec le rand corrigé faites dans un topic précédent l'ont démontré (et, non Dlzlogic, ces fonctions rand corrigées ne font pas exprès de suivre une loi normale puisqu'elles sont censées modéliser le plus fidèlement possible une loi uniforme).
Dlzlogic a écrit:Concernant la moyenne :
Le théorème central limite précise "moyenne empirique", et donne sa formule qui est la moyenne arithmétique.
Pour exprimer la même chose, vers les années 1960, on disait "postulat de la moyenne" et on ajoutait que c'était la moyenne arithmétique.
Donc il semble bien qu'on parle de la même chose.
Jusqu'à présent (ou alors j'ai raté quelque chose), quand on te demandait ce qu'était le postulat de la moyenne, tu répondais "lors d'une série de tirages aléatoires, la moyenne arithmétique des résultats est la valeur la plus probable". Cette phrase telle quelle est complètement fausse et on t'a sorti des tonnes d'exemples, le plus simple étant un tirage suivant une loi uniforme entre deux valeurs chiffrées, 0 et 1 par exemple. La moyenne arithmétique des résultats sera très certainement un nombre non entier entre 0 et 1 qui ne sera jamais atteignable comme résultat du tirage. Face à cet argument on ne peut plus simple, ta riposte classique c'est "ouais mais au lieu de tirer 0 et 1 j'aurais pu tirer A et B ou renard et chimpanzé et évidemment la moyenne n'a pas de sens". Même s'il est vrai que ça n'a pas de sens de parler de la moyenne arithmétique d'un renard et d'un chimpanzé, tu ne réponds pas du tout à l'argument qui pointe ton manque cruel de rigueur et de compréhension des mots que tu emploies (de la part de quelqu'un qui fait sans cesse l'éloge du raisonnement scientifique, de la rigueur et de la valeur des démonstrations, c'est un comble).
Ce qui est une conséquence du théorème central limite (en fait, c'est surtout la loi des grands nombres qui dit ça, mais ici ça importe peu), ce n'est PAS "lors d'une série de tirages aléatoires, la moyenne arithmétique est des résultats est la valeur la plus probable", c'est "lors d'une série de N tirages aléatoires
INDÉPENDANTS ET SUIVANT LA MÊME LOI DE PROBABILITÉ, qui portent sur des nombres réels, avec N suffisamment grand, la valeur la plus probable de
LA MOYENNE DES RÉSULTATS DES N TIRAGES est l'espérance de la loi de probabilité en question".
Les passages que j'ai mis en gras majuscule ne sont pas là pour décorer, ils sont absolument fondamentaux, et ils font que ça ne dit pas du tout la même chose que ton postulat de la moyenne. Cette deuxième phrase entre guillemets ne dit pas non plus que "la répartition des écarts à la moyenne suit une loi normale", elle dit que "la répartition des écarts
de la moyenne arithmétique des résultats des tirages à l'espérance de loi suit une loi qui ressemble à une loi normale".
Le véritable énoncé du TLC emploie des termes plus précis (il utilise notamment une définition claire de "ressembler à une loi normale").
Dlzlogic a écrit:@ Sylviel,
Dans tes deux dernières réponses, il n'apparait pas très clairement si tu fais la somme des valeurs de faces sorties puis leur moyenne ou le comptage des nombre de sorties de chaque face, la moyenne étant forcement connue, puisque c'est le nombre de tirages divisé par 6.
Dans la première hypothèse, c'est à dire celle qu'on lit, que se passerait-il s'il s'agissait de dés à jouer pour enfant, où au lieu de nombres, on aurait mis des images d'animaux ?
Dans son exemple, Sylviel fait la somme des valeurs sur les faces. En effet, cette opération n'est pas possible si ce ne sont pas des nombres sur les faces puisque le théorème central limite parle de variables aléatoires réelles. C'est pourquoi on cherche souvent à se ramener à des nombres réels, par exemple en comptant le nombre de sorties de chaque face, indépendamment de ce qu'il y a écrit dessus. Mais là on change de variable aléatoire, on change de loi.
J'ai un dé classique dont les 6 faces sont désignées par les chiffres de 1 à 6. Je fais N lancers consécutifs de ce dé. Au k-ième lancer j'associe la variable aléatoire "résultat du k-ième lancer", que je note par exemple
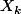
qui suit une loi uniforme sur l'ensemble {1,2,3,4,5,6}. Là-dessus je peux appliquer le théorème central limite (parce que je suis bien en présence d'une suite de variables aléatoires réelles de même loi et que les tirages sont supposés indépendants, ce qui au passage signifie justement que le dé ne se souvient pas de ce qu'il a sorti avant) : si je fais la moyenne arithmétique des
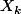
(qui est donc un nombre entre 1 et 6), la probabilité d'obtenir un nombre m est d'autant plus faible que m est éloigné de 21/6, et elle diminue à peu près comme en suivant une gaussienne.
J'ai maintenant un dé exotique dont les 6 faces sont désignées par 1, 2, 3, 4, 5 et 100. Les
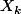
suivent cette fois la loi uniforme sur {1,2,3,4,5,100}. Le théorème central limite s'applique toujours aux variables "résultat du k-ième lancer" : si je fais la moyenne arithmétique des
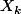
(qui est donc un nombre entre 1 et 100), la probabilité d'obtenir un nombre m est d'autant plus faible que m est éloigné de 115/6, et elle diminue à peu près comme en suivant une gaussienne.
Je passe maintenant à un dé dont les 6 faces sont désignées par les lettres de A à F. Les
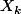
suivent cette fois la loi uniforme sur {A,B,C,D,E,F}. Le théorème central limite ne s'applique pas aux
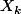
puisque ce ne sont pas des variables aléatoires réelles. Pour pallier ce problème je peux par exemple m'intéresser à une autre suite de variables aléatoires, par exemple la variable
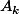
qui vaut 1 si le résultat du k-ième lancer est A, et 0 sinon.
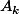
suit une loi binomiale. Cette fois-ci je peux appliquer le théorème central limite : si je fais la moyenne arithmétique des
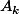
(c'est-à-dire si je calcule la fréquence d'apparition de la face A sur mes N tirages), la probabilité d'obtenir un nombre m est d'autant plus faible que m est éloigné de 1/6, et elle diminue à peu près comme en suivant une gaussienne.
Dlzlogic a écrit:Le texte du théorème est très clair, il s'agit de la répartition des nombres des écarts à la moyennes, suivant la constatation que plus cet écart à la moyenne est grand, moins il a de chances d'arriver.
Encore une fois, c'est faux tel que tu le dis, et c'est tout sauf clair : le nombre des écarts DE QUOI à la moyenne DE QUOI ?
