Bonsoir : :happy3:
C'est simple à comprendre : :happy3:
Généralement, on intègre un élément de volume qui est sous la forme :
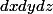
. En coordonnées sphériques, cela revient à intégrer un élément de volume sous la forme
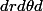
. ( intégrer sur une boule, en coordonnées cartésiennes, veut dire, parcourir tous les points de la boule
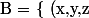 \in \mathbb{R} \ / \ ||(x,y,z)|| \leq 1 \} $)
,en langage courant :zen: )
Cela se fait en

étapes :
 $)
D'abord, on intégre par rapport à
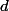
, on parcourt ( intégre ) tous les points d'un cercle parallèle au plan
 $)
, c'est à dire,
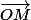
fait un tour complet d'angle :
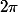
sur le cercle, c'est à dire
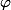
fait un tour de

à
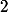
pour parcourir ( intégrer ) tous les points du cercle ...
 $)
Ensuite, on integre par rapport à
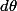
pour parcourir tous les cercles possibles, parallèles au plan
 $)
, et pour parcourir tous les cercles possibles, on va du pôle sud vers le pôle nord, c'est à dire
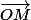
fait un demi tour ( on parcours un demi - cercle ), allant du pôle sud

vers le pôle nord
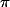
, c'est à dire on parcours un angle qui mesure
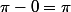
.
Jusqu'ici, on a intégré globalement, par rapport à
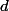
et par rapport à
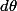
, c'est à dire, on a integré, en somme, un élément de surface
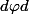
, et donc, on a parcouru toute une sphère ( on a parcouru tous les points d'une sphère ).
 $)
Il reste maintenant à parcourir tous les sphères parallèles d'origines

de rayon
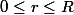
, qui composent la boule d'origine

et de rayon

, pour cela, on intègre par rapport à
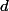
, c'est à dire,

va de

à

. Ce qui fait finalement qu'on a parcouru tous les points de la boule unité, c'est à dire, on a parcouru ( intégré ) un élément de volume
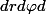
sur
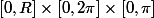
.
J'espère que c'est claire. :happy3:
