Nombres complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Nov 2011, 02:32
par mehdi-128 » 04 Nov 2011, 02:32
Bonsoir,
on me demande de résoudre :
^{2n}-1=0)
J'ai fait :
^{2n}=1)
Je retrouve les racines n-ièmes de l'unité.
Je pose :
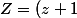^2)
Je dois donc résoudre :
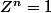
Les solutions sont de la forme :
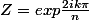
Avec k compris entre 0 et n-1.
Or :
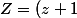^2)
D'où :
^2=exp{\frac{2ik\pi}{n}})
Donc :
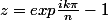
ou
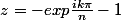
C'est correct ?
Pour la suite, on note :

les racines de l'équation précédente.
Montrer que :
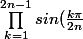=- \frac{\prod_{k=1}^{2n-1}z_k}{2^{2n-1}})
Là je bloque.
Merci.
-
mathelot
 par mathelot » 04 Nov 2011, 07:44
par mathelot » 04 Nov 2011, 07:44
mehdi-128 a écrit:^{2n}=1)
Je retrouve les racines n-ièmes de l'unité.
il y a plus simple: ce sont les racines 2n-ièmes ?
donc
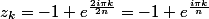
ensuite habituellement, on factorise
l'arc moitié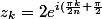} \, sin(\frac{\pi k}{2n}))
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Nov 2011, 19:41
par mehdi-128 » 04 Nov 2011, 19:41
mathelot a écrit:il y a plus simple: ce sont les racines 2n-ièmes ?
donc
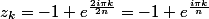
ensuite habituellement, on factorise
l'arc moitié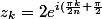} \, sin(\frac{\pi k}{2n}))
J'ai pas trop compris comment vous avez factorisé
-
laya
- Membre Relatif
- Messages: 128
- Enregistré le: 06 Déc 2010, 20:12
-
 par laya » 04 Nov 2011, 19:54
par laya » 04 Nov 2011, 19:54
mehdi-128 a écrit:J'ai pas trop compris comment vous avez factorisé
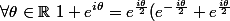)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Nov 2011, 20:16
par mehdi-128 » 04 Nov 2011, 20:16
laya a écrit: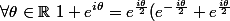)
Merci :id:
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Nov 2011, 21:44
par mehdi-128 » 04 Nov 2011, 21:44
J'ai pas réussi à démontrer :
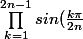=- \frac{\prod_{k=1}^{2n-1}z_k}{2^{2n-1}})
Je sais que :
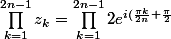} \, sin(\frac{\pi k}{2n}))
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 04 Nov 2011, 23:36
par mehdi-128 » 04 Nov 2011, 23:36
help :mur:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
