Exercice nombres complexes
15 messages
- Page 1 sur 1
exercice nombres complexes
Bonjour tout le monde !
Je suis en prépa BCPST-VETO, et je me permet de solliciter votre aide dans le cadre d'un exercice que j'ai à faire, il s'agit de nombres complexes ... et je suis complètement bloqué, déjà pas très matheuse à la base (pourtant j'me bat j'vous jure !) je n'arrive pas à démarrer ! :cry: Je vous donne l'énoncé en entier et si quelqu'un pouvait me donner une piste pour démarrer ce serait vraiment gentil ...
On considère le nombre complexe z = cos (2pi)/7 + i sin (2pi)/7 (encore noté exp ( i (2pi)/7).
On admet la formule de De Moivre.
1) On pose S = z+z^2+z^4 et T=z^3+z^5+z^6.
Montrer que cos (12pi/7)=cos(2pi/7) et sin(12pi/7)=- sin (2pi/7).
En déduire que zbar = z^6.
2)Calculerz^7 puis montrer que S et T sont conjugués.
3) Calculer S+T. penser aux suites géométriques.
4) Calculer U=cos(2pi/7) + cos (4pi/7) + cos(8pi/7).
je cherche désespèrèment la question 1 pourtant je pense que le début ne doit pas être compliqué ... donc je vous remercie d'avance du coup de pouce que vous pourriez me donner ! :we:
Je suis en prépa BCPST-VETO, et je me permet de solliciter votre aide dans le cadre d'un exercice que j'ai à faire, il s'agit de nombres complexes ... et je suis complètement bloqué, déjà pas très matheuse à la base (pourtant j'me bat j'vous jure !) je n'arrive pas à démarrer ! :cry: Je vous donne l'énoncé en entier et si quelqu'un pouvait me donner une piste pour démarrer ce serait vraiment gentil ...
On considère le nombre complexe z = cos (2pi)/7 + i sin (2pi)/7 (encore noté exp ( i (2pi)/7).
On admet la formule de De Moivre.
1) On pose S = z+z^2+z^4 et T=z^3+z^5+z^6.
Montrer que cos (12pi/7)=cos(2pi/7) et sin(12pi/7)=- sin (2pi/7).
En déduire que zbar = z^6.
2)Calculerz^7 puis montrer que S et T sont conjugués.
3) Calculer S+T. penser aux suites géométriques.
4) Calculer U=cos(2pi/7) + cos (4pi/7) + cos(8pi/7).
je cherche désespèrèment la question 1 pourtant je pense que le début ne doit pas être compliqué ... donc je vous remercie d'avance du coup de pouce que vous pourriez me donner ! :we:
question 2
Bonjour Luciole
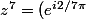^7=e^{i2\pi}=1) (c'est une autre manière d'exprimer la formule de Moivre.
(c'est une autre manière d'exprimer la formule de Moivre.
Alors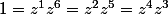 , on a que:
, on a que:
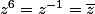
etc. en sommant tu obtiendras la réponse.
Alors
etc. en sommant tu obtiendras la réponse.
Oui j'ai utilisé cette formule après m'être servie de celle de la somme d'une suite géométrique et j'ai trouvé S+T=0. Je suis à présent à la question 4 et je suppose que pour le calcul de U il faut se servir de la périodicité des fonctions sinus et cosinus comme pour la question 1. Je vais y arriver ! (motivée ! :we: )
Encore merci ^^
Encore merci ^^
Luciole a écrit:Oui j'ai utilisé cette formule après m'être servie de celle de la somme d'une suite géométrique et j'ai trouvé S+T=0. Je suis à présent à la question 4 et je suppose que pour le calcul de U il faut se servir de la périodicité des fonctions sinus et cosinus comme pour la question 1. Je vais y arriver ! (motivée ! :we: )
Encore merci ^^
Ce n'est pas 0 la réponse. Il faut utiliser la formule pour
J'ai beau refaire le calcul encore et encore je trouve toujours la même chose ... :triste:
J'ai fait : S+T = z +z^2+z^3+z^4+z^5+z^6
on remarque qu'il s'agit là de la somme des n=6 premiers termes d'une suite géométrique de raison q=z.
La somme vaut : S+T = 1*(1+z+...+z^6)
d'après la formule : S+T= (z^7-1)/(z-1)
J'ai trouvé z^7=1 donc S+T = O ....
Par ailleurs pour la question 2 pour montrer que S et T sont conjugués je suis passée trop vite et et j'ai fait n'importe quoi .. :briques: j'ai commencé par calculer les sommes S et T mais je ne pense pas que cela soit indispensable ?!
Chui dsl j'abuse encore de vous mais si vous avez une piste (ça semble si facile pour vous ! :id: ) je ne crache pas dessus ...
Merci ! :we:
J'ai fait : S+T = z +z^2+z^3+z^4+z^5+z^6
on remarque qu'il s'agit là de la somme des n=6 premiers termes d'une suite géométrique de raison q=z.
La somme vaut : S+T = 1*(1+z+...+z^6)
d'après la formule : S+T= (z^7-1)/(z-1)
J'ai trouvé z^7=1 donc S+T = O ....
Par ailleurs pour la question 2 pour montrer que S et T sont conjugués je suis passée trop vite et et j'ai fait n'importe quoi .. :briques: j'ai commencé par calculer les sommes S et T mais je ne pense pas que cela soit indispensable ?!
Chui dsl j'abuse encore de vous mais si vous avez une piste (ça semble si facile pour vous ! :id: ) je ne crache pas dessus ...
Merci ! :we:
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
