Forme quadratique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 17 Fév 2010, 18:06
par Kimou » 17 Fév 2010, 18:06
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Fév 2010, 18:15
par girdav » 17 Fév 2010, 18:15
Si je résume bien on a pour
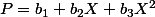
que
 = b_1^2+b_1b_2+b_1b_3 = \(b_1-\fr 12 b_2-\fr 12b_3\)^2-\cdots)
.
Tu as trouvé quoi comme signature?
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 17 Fév 2010, 18:29
par Kimou » 17 Fév 2010, 18:29
girdav a écrit:Si je résume bien on a pour
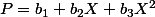
que
 = b_1^2+b_1b_2+b_1b_3 = \(b_1-\fr 12 b_2-\fr 12b_3\)^2-\cdots)
.
Tu as trouvé quoi comme signature?
oui
)
c'est bien cela.
Nous n'avions pas eu besoin de faire de réduction de Gauss jusque là. La signature nous ne l'avons pas fait... ou je ne l'ai pas noté, ce qui est possible car j'essayais de comprendre cette résolution^^
Quant à la resolution du prof c'était en ce basant sur le fait qu'on connaisse la matrice dans cette nouvelle base (jusque là no pb) et puis il fait des sytèmes en disant que
=1 et b(P_0,P_1)=0)
etc... lui en ayant l'habitude a trouver les résultats assez rapidement et moi en me relançant dedans je m'y perd avec tous ces sytemes.
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 17 Fév 2010, 18:44
par Kimou » 17 Fév 2010, 18:44
girdav a écrit:Si je résume bien on a pour
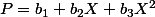
que
 = b_1^2+b_1b_2+b_1b_3 = \(b_1-\fr 12 b_2-\fr 12b_3\)^2-\cdots)
.
Tu as trouvé quoi comme signature?
oui
)
c'est bien cela.
Nous n'avions pas eu besoin de faire de réduction de Gauss jusque là. La signature nous ne l'avons pas fait... ou je ne l'ai pas noté, ce qui est possible car j'essayais de comprendre cette résolution^^
Quant à la resolution du prof c'était en ce basant sur le fait qu'on connaisse la matrice dans cette nouvelle base (jusque là no pb) et puis il fait des sytèmes en disant que
=1 et b(P_0,P_1)=0)
etc... lui en ayant l'habitude a trouver les résultats assez rapidement et moi en me relançant dedans je m'y perd avec tous ces sytemes.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Fév 2010, 18:48
par girdav » 17 Fév 2010, 18:48
Mais il y a une chose qui me chiffonne : avec la réduction de Gauss on voit que la signature est
)
alors qu'il semblerait d'après la question qu'il s'agit de
)
.
Comme elle ne dépend pas de la base, libre à toi de décider qui a tort et qui a raison.
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 17 Fév 2010, 18:57
par Kimou » 17 Fév 2010, 18:57
girdav a écrit:Mais il y a une chose qui me chiffonne : avec la réduction de Gauss on voit que la signature est
)
alors qu'il semblerait d'après la question qu'il s'agit de
)
.
Comme elle ne dépend pas de la base, libre à toi de décider qui a tort et qui a raison.
Oui mais tu as fait la reduction sur q(p) dans la base canonique et non la nouvelle base?
La signature ne peut de toute facon pas être (1,2) dans aucun des cas parce que les 2 matrices que ca soit dans l'une ou l'autre base ne sont pas de rang 3...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Fév 2010, 19:01
par girdav » 17 Fév 2010, 19:01
Exact, j'ai essayé de faire la réduction de tête, en oubliant le double produit

. Ceci donne bien que la signature est
)
.
On trouve dans la réduction que
 = \(b_1-\fr 12b_2-\fr 12 b_3\)^2 -<br />\fr 14 b_2^2-\fr 14b_3^2 + \fr 12b_2b_3 <br />=\(b_1-\fr 12b_2-\fr 12 b_3\)^2 -\fr 14\(b_2-b_3\)^2)
ce qui est plus cohérent.
On a quasiment notre nouvelle base maintenant.
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 17 Fév 2010, 19:18
par Kimou » 17 Fév 2010, 19:18
On a quasiment notre nouvelle base maintenant.
Peux tu m'expliquer? a partir d'une réduction de gauss je sais trouver une base orthogonale mais une base dont l'expression m'est imposée je sèche un peu...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Fév 2010, 19:29
par girdav » 17 Fév 2010, 19:29
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 17 Fév 2010, 19:43
par Kimou » 17 Fév 2010, 19:43
génial je te remercie beaucoup!
J'avais commencer par faire la technique de la transposée ca me paraissait mieux et je savait aps comment trouver P...
Merci!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
