Eq diff avec second membre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 10 Fév 2010, 08:28
par MacErmite » 10 Fév 2010, 08:28
Bonjour,
Je tente de résoudre cette eq. diff :

sur R+ *,mais je doute sur le résultat que j'ai sous les yeux ....
1/ J'ai commencé par résoudre

d'ou
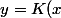.x^2)
.
Ensuite si je dérive ce résultat :
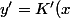.x^2+K(x).2x)
2/ Si

alors :
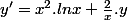
3/ Après en identifiant chaque membre :
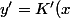.x^2+K(x).2x = x^2.ln x+\frac{2}{x}.K(x).x^2)
je trouve
 = ln x)
, soit
=x.ln x - x+c)
4/ Cela conduit à :
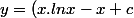.x^2)
:doh:
Ai-je la bonne démarche ? Ce résultat vous semble-t-il juste ?
Merci

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Fév 2010, 10:05
par Ben314 » 10 Fév 2010, 10:05
Il y a forcément une erreur (dans la solution de l'équation homogène : je te laisse la trouver, c'est bébète...) :
Dans la méthode "de variation de la constante" où on pose y=k.yo (yo sol. de l'équation homogène, k fonction) on a y'=k'.yo+k.yo' et la partie en k.yo' doit forcément s'éliminer quand on substitue car elle correspond à la dérivée de k.yo dans le cas ou k est constant et, par hypothèse concernant le yo, le terme "de gauche" doit valoir 0 lorsque y=k.yo avec k constant.
Il n'est donc pas normal qu'il te reste du "k" aprés substitution : il ne devrait y avoir que du k'.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mathelot
 par mathelot » 10 Fév 2010, 12:24
par mathelot » 10 Fév 2010, 12:24
re,
ça serait pas plutot
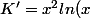)
et après une primitive obtenue en intégrant par parties
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 10 Fév 2010, 15:27
par MacErmite » 10 Fév 2010, 15:27
mathelot a écrit:re,
ça serait pas plutot
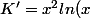)
et après une primitive obtenue en intégrant par parties
Comment as-tu obtenu cette expression de K' ?
 par alavacommejetepousse » 10 Fév 2010, 15:35
par alavacommejetepousse » 10 Fév 2010, 15:35
bonjour
variation de la constante
ay' +by = c (1)
si y0 est solution de ay'+by= 0 (0)
en posant y = ky0
y est solution de (1) ssi ak'y0 = c
fais le de façon littérale
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 11 Fév 2010, 18:29
par MacErmite » 11 Fév 2010, 18:29
Merci pour vos réponses.
J'ai repris cet exercice et je me demande si j'effectuais la démarche inverse ne pourrais-je pas retrouver l'énnoncé ?
Si
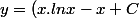. x^2)
en dérivant y; on obtien :
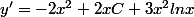
Ensuite en reprenant l'eq diff en question :
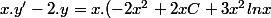 -2.((x.ln x -x + C). x^2) = ...= x^3.ln x)
:marteau:
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 11 Fév 2010, 23:14
par MacErmite » 11 Fév 2010, 23:14
alavacommejetepousse a écrit:pourquoi pas
On peut faire une erreur sur la détermination de y, et obtenir avec cette fonction le résultat du second membre ? :help:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités