100 urnes à trier
24 messages
- Page 1 sur 2 - 1, 2
100 urnes à trier
Bonsoir :zen:
Trois problèmes pour le prix d'un , les deux premiers sont déjà bien amusants et le troisième est un vrai casse-tête :marteau:
1°) 99 urnes contiennent des boules bleues et des boules rouges . Montrer que l'on peut choisir 50 de ces urnes de façon à ce qu'elles contiennent au moins la moitié des boules bleues et la moitié de boules rouges .
2°) 100 urnes contiennent des boules bleues et des boules rouges . Montrer que l'on peut choisir 34 de ces urnes de façon à ce qu'elle contiennent au moins un tiers des boules bleues et un tiers des boules rouges .
3°) 100 urnes contiennent des boules bleues , des boules blanches et des boules rouges . Montrer que l'on peut choisir 51 de ces urnes de façon à ce qu'elles contiennent au moins la moitié des boules bleues , la moitié des boules blanches et la moitié des boules rouges .
Amusez-vous bien :zen:
Imod
Trois problèmes pour le prix d'un , les deux premiers sont déjà bien amusants et le troisième est un vrai casse-tête :marteau:
1°) 99 urnes contiennent des boules bleues et des boules rouges . Montrer que l'on peut choisir 50 de ces urnes de façon à ce qu'elles contiennent au moins la moitié des boules bleues et la moitié de boules rouges .
2°) 100 urnes contiennent des boules bleues et des boules rouges . Montrer que l'on peut choisir 34 de ces urnes de façon à ce qu'elle contiennent au moins un tiers des boules bleues et un tiers des boules rouges .
3°) 100 urnes contiennent des boules bleues , des boules blanches et des boules rouges . Montrer que l'on peut choisir 51 de ces urnes de façon à ce qu'elles contiennent au moins la moitié des boules bleues , la moitié des boules blanches et la moitié des boules rouges .
Amusez-vous bien :zen:
Imod
Imod a écrit:Pas mal du tout nodgim :++:
Il reste à affiner un tout petit peu ta stratégie en supposant par exemple que les urnes sont initialement classées de celle qui contient le plus de bleus à celle qui en contient le moins . Sinon l'idée est là !!!
Imod
C'est volontairement que j'ai donné une solution avec des trous, pour laisser un peu de mystère à ceux qui s'y intéressent. :++:
Bon , je donne une réponse pour le premier problème histoire de remotiver les troupes !
On suppose que les urnes sont classées par ordre décroissant de boules bleues . On prend alors l'urne
sont classées par ordre décroissant de boules bleues . On prend alors l'urne  puis parmi
puis parmi 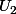 et
et  « celle » qui contient le plus de boules rouges puis parmi
« celle » qui contient le plus de boules rouges puis parmi 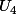 et
et 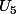 « celle » qui contient le plus de boules rouges ... puis parmi
« celle » qui contient le plus de boules rouges ... puis parmi  et
et  « celle » qui contient le plus de boules rouges . Il est clair quon a pris plus de boules rouges quon en a laissé et si on note
« celle » qui contient le plus de boules rouges . Il est clair quon a pris plus de boules rouges quon en a laissé et si on note 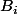 le nombre de boules bleues dans lurne
le nombre de boules bleues dans lurne 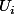 , dans le pire des cas on a pris
, dans le pire des cas on a pris  boules bleues . Or
boules bleues . Or  , on a donc pris au moins la moitié des bleues .
, on a donc pris au moins la moitié des bleues .
Reste les deux autres problèmes
Imod
On suppose que les urnes
Reste les deux autres problèmes
Imod
Imod a écrit:Bon , je donne une réponse pour le premier problème histoire de remotiver les troupes !
On suppose que les urnessont classées par ordre décroissant de boules bleues . On prend alors l'urne
puis parmi
et
« celle » qui contient le plus de boules rouges puis parmi
et
« celle » qui contient le plus de boules rouges ... puis parmi
et
« celle » qui contient le plus de boules rouges . Il est clair quon a pris plus de boules rouges quon en a laissé et si on note
le nombre de boules bleues dans lurne
, dans le pire des cas on a pris
boules bleues . Or
, on a donc pris au moins la moitié des bleues .
Reste les deux autres problèmes
Imod
Tiens j'avais fait plus simple! :doh:
Je garde par devers moi le plus gros bleu. Je trie les autres bleus du plus gros au plus petit. Je prends alors les bleus 2 par 2 et j'équilibre au mieux. A la fin, je regarde où est la majorité des rouges, et je mets le gros bleu de réserve dans la moitié majoritaire rouge.
Un essai pour le 3)
Je trie les bleus et les rouges, je ne m'occupe pas des blancs.
Je vérifie d'abord qu'il n'y a pas un tiroir qui à lui seul contiendrait plus de la moitié de tous les autres dans une couleur donnée. La stratégie serait alors facilitée, mais il faudrait procéder autrement.
Donc je prends les 2 plus gros bleus et je les mets chacun dans un des 2 tas que je vais constituer. Je prends ensuite les 2 plus gros rouges et je fais le choix en fonction des bleus qui les accompagnent, car c'est eux qui en principe auront le plus gros écart. Je prends ensuite les 2 plus gros bleus et je fais le même choix que précédemment. En procédant ainsi, j'aurais bien à la fin au moins un tiers de bleus et de rouges dans chaque tas. Ensuite, il ne reste qu'a choisir le tas qui comporte au moins un tiers de blancs.
Je trie les bleus et les rouges, je ne m'occupe pas des blancs.
Je vérifie d'abord qu'il n'y a pas un tiroir qui à lui seul contiendrait plus de la moitié de tous les autres dans une couleur donnée. La stratégie serait alors facilitée, mais il faudrait procéder autrement.
Donc je prends les 2 plus gros bleus et je les mets chacun dans un des 2 tas que je vais constituer. Je prends ensuite les 2 plus gros rouges et je fais le choix en fonction des bleus qui les accompagnent, car c'est eux qui en principe auront le plus gros écart. Je prends ensuite les 2 plus gros bleus et je fais le même choix que précédemment. En procédant ainsi, j'aurais bien à la fin au moins un tiers de bleus et de rouges dans chaque tas. Ensuite, il ne reste qu'a choisir le tas qui comporte au moins un tiers de blancs.
ffpower a écrit:en effet,soit le tas U1,U3,U5....,U99 marche,soit le tas U1,U2,U4...,U98 marche
Edit:faut plus que tu postes nodgim,666 messages c est classe.
Edit2:ah ben trop tard,tant pis lol
Bah, tout le monde est passé par là un jour ou l'autre :happy2:
Qu'espérer maintenant, comme nombre remarquable ? 1729, par exemple ?
Je ne donne pas spécialement priorité aux rouges, mais alternativement aux rouges et aux bleus. Un exemple:
Je prends les 2 plus gros bleus: (100B 25R) (95B 78R)
Je prends les 2 plus gros rouges: (90R 3B) (90R 56B)
Je groupe selon la moindre différence TOTAL: (103B,115R)(98B,168R)
Je prends à nouveau les 2 plus gros bleus: (94B, 13R) (93B, 88R)
Je groupe selon la moindre différence:
TOTAL: (196B, 203R) (192B, 181B)
Je prends les 2 plus gros rouges, etc..
En fait je vise à l'équilibre, pour être sûr d'avoir au moins 1/3 de chaque coté.
Ensuite il n'y plus à la fin qu'à choisir le coté majoritaire blanc.
Gros problème avec cette méthode: aucun moyen de quantifier au final la proportion exacte des bleus et des rouges de part et d'autre. En particulier, aucun moyen de vérifier que le 1/3 est atteint. Avec 100 urnes, ça semble assez évident, mais....
Je prends les 2 plus gros bleus: (100B 25R) (95B 78R)
Je prends les 2 plus gros rouges: (90R 3B) (90R 56B)
Je groupe selon la moindre différence TOTAL: (103B,115R)(98B,168R)
Je prends à nouveau les 2 plus gros bleus: (94B, 13R) (93B, 88R)
Je groupe selon la moindre différence:
TOTAL: (196B, 203R) (192B, 181B)
Je prends les 2 plus gros rouges, etc..
En fait je vise à l'équilibre, pour être sûr d'avoir au moins 1/3 de chaque coté.
Ensuite il n'y plus à la fin qu'à choisir le coté majoritaire blanc.
Gros problème avec cette méthode: aucun moyen de quantifier au final la proportion exacte des bleus et des rouges de part et d'autre. En particulier, aucun moyen de vérifier que le 1/3 est atteint. Avec 100 urnes, ça semble assez évident, mais....
Je t'avais bien compris nodgim , je parlais du dernier choix :we:
Je te rappelle que ce n'est pas 1/3 mais 1/2 qu'il faut atteindre :marteau:
Imod
nodgim a écrit:Gros problème avec cette méthode: aucun moyen de quantifier au final la proportion exacte des bleus et des rouges de part et d'autre. En particulier, aucun moyen de vérifier que le 1/3 est atteint. Avec 100 urnes, ça semble assez évident, mais....
Je te rappelle que ce n'est pas 1/3 mais 1/2 qu'il faut atteindre :marteau:
Imod
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
