Petite question

[Aurelie57]

voila je voudrais savoir comment trouver le sens de variation de la fonction


(4-3x)^5


je suis en 1ere avec la dérivée impossible de trouver
et j'arrive pas a trouver avec les composées de fonctions

[Benjamin]

Bonjour,
Tu peux trouver avec la dérivée sans problème normalement. Qu'as-tu trouvé comme dérivée ?
Ensuite, pense que y^4, c'est (y²)².

[Aurelie57]

Mais en fait ce que je me demandais c'est

x^n = n.x^n-1


or la c'est plus x mais la fonction u(x)= 4-3x qu'on qui est élevée a la puissance 5


donc d'apres toi on peut faire (4-3x)^5 a pour dérivée

5(4-3x)^4 ?

[Aurelie57]

Mais en fait ce que jaimerai pouvoir faire c'est

si une fois derivée ma fonction je trouve
(4-3x)^5


après la je fais comment pour etudier sa variation?

merci de ton aide

[Benjamin]

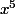
Effectivement, la dérivée de est différente de la dérivée de . En fait, . Quelle est donc la dérivée de ta fonction ?

[Aurelie57]

ca me donne -15*(4-3x)^4


ok apres je peux arriver parce que cest puissance 4

mais si jamais la puissance est très grande n'y a t'il pas un moyen
autre que la derivée?

[chan79]

salut
je voudrais faire remarquer que la fonction x---->-3x+4 est décroissante sur R
et que la fonction x--->x^5 est croissante sur R (sa dérivée est 4 x^4)
donc on peut conclure facilement

[rene38]

Bonjour

Exposant 4 ou 2008, c'est pareil pour le signe.

[chan79]

si n est un entier impair, x^n est croissante sur R.