J'ai besoin d'aide

[hiller]

bonjour;Ca fais 6ans que je n'ai pas fais de math il faut que je rende cette exercice pouvez vous m'aider????Merci
voici mon exercice:
Soit E=]-~;-1[u]-1;3[u]3;+~[ et f la fonction definie sur E par:
f(x)=4x²-8x/x²-2x-3
on designe par (C) la courbe representative de f dans un repere orthogonal(O;i;j)
on prendra pour unité graph:2cm en abscisse et 1cm par ordonnée.
1)justifier que la fonction est bien définie sur E
2)Etudier les limites de f à l'infini.En déduire que la courbe C possède une asymptote horizontale delta dt on donnera l'equation
3)determiner les limites de f en -1 et en 3.que peut on en deduire
4)montrer que la fonction derivee f' est definie sur E par f'(x)=24(-x+1)/(x²-2x-3)² en deduire le tableau de variation de la fonction f
5)Soit la tangente a la courbe(C) au point d'origine du repere.Determener une equation de T
6)Tracer les asymptotes,la tangente T et la courbe C
7)Verifier que pr tout x de E,f(x)-8/3x=-8x3+28x²/3(x²-2x-3)
en dedire les coordonnees des pts communs a T et a (C)
Determiner les positions relatives de la tangente T et de la courbe (C)

[maf]

1) f(x) est définie si le dénominateur est différent de 0
x²-2x-3 (factoriser en trouvant une racine par ex. -1) ou alors utiliser la formule du second degré

[fonfon]

salut,

Soit E=]-~;-1[u]-1;3[u]3;+~[ et f la fonction definie sur E par:
f(x)=4x²-8x/x²-2x-3
on designe par (C) la courbe representative de f dans un repere orthogonal(O;i;j)
on prendra pour unité graph:2cm en abscisse et 1cm par ordonnée.
1)justifier que la fonction est bien définie sur E

on peut ecrire que:




donc il faut que (x-3)(x+1) soit different de 0 pour qe f soit definie donc il faut que x soit different de 3 ou de -1 donc Df=]-inf,-1[U]-1,3[U]3,+inf[=E

2)Etudier les limites de f à l'infini.En déduire que la courbe C possède une asymptote horizontale delta dt on donnera l'equation

et


car en +inf ou -inf une fonction rationnelle a la même limite que le quotient de ses termes de plus haut degré

donc la droite d'equation y=4 est asymptote au voisinage de

tu es sûr de rien pouvoir proposer pour la suite?

[hiller]

en faites le truc c'est que je me souviens plus du tout des methodes de resolution

[hiller]

la je bosse les cours pour m'y remettre mais j'ai ce devoir a rendre et je n'y arrive pas

[fonfon]

re,

as-tu compris comment j' ai factotiser f(x) en

on peut ecrire que:

[hiller]

tu as resolu les 2 equations

[hiller]

par contre comment es ce que je peux tracer ma courbe?

[fonfon]

tu as resolu les 2 equations

non , il n'y a pas d'equation


j'ai factorisé le numerateur par 4x soit 4x²-8x=4x(x-2) et pour le denominateur j'ai utilisé le discriminant

on fait en remplaçant par les vaeurs on a:

donc 2 racines réelle
ou
ou

donc


d'où

par contre comment es ce que je peux tracer ma courbe?

avant de faire ceci tu as réussi les autres questions?

[hiller]

non je n'y arrive pas du tout ca peu paraitre surprenant mais j'ai beaucoup de mal!j'ai tenté de resoudre la 3 et je suis bloqué

[fonfon]

3)determiner les limites de f en -1 et en 3.que peut on en deduire

il faut etudier les limites en -1-,-1+,3- et 3+
donc

en -1-:



donc

en -1+:



donc


en 3-:


donc

en 3+:



donc


ce que l'on peut en deduire c'est que les droites d'equations x=-1 et x=3 sont asymptotes à la courbe au voisinage de

[hiller]

Sans abuser peux tu m'aider a resoudre le reste des questions?

[fonfon]

4)montrer que la fonction derivee f' est definie sur E par f'(x)=24(-x+1)/(x²-2x-3)² en deduire le tableau de variation de la fonction f

f est de la forme de derivée
donc
pour tout x ds E,







d'où le resultat recherché

ensuite f'(x) est du signe de -x+1 car sur E

donc maintenant essaie de trouver le signe de la derivée qui te donneront les variations de ta fonction


je dois partir , si c'est pas urgent je passerais demain matin sinon quelqu'un peut prendre le relais

[hiller]

merci beaucoup de ton aide c'est assez urgent car je dois le rendre vendredi mais si demain matin tu peux m'aider je suis pour mais merci deja pour ton aide

[hiller]

:help: par contre si quelqu'un peu continuer a m'aider

[fonfon]

donc comme je l'ai dit pls jaut f'(x) est du signe de -x+1 sur E on peut faire un tableau de signe




donc f est croissante sur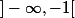 et sur ]-1,1[, decroissante sur ]1,3[ et sur

d'où le tableaude variation:



reste à mettre dans le tableau les limites (aux extremites des fleches) trouvés dans les questions precedentes

[hiller]

merci pour la suite pourrez tu m'aider à finir l'exercice?

[fonfon]

5)Soit la tangente a la courbe(C) au point d'origine du repere.Determener une equation de T

formule: equation de la tangente au point d'abscisse est


donc ici on veut la tangente au point d'origine donc de coordonnées O(0,0) donc ici

donc l'equation de la tangente est: on calcule f'(0) et f(0)

on connait donc ensui te on calcule donc il ne reste plus qu'à remplacer dans l'equation soit:




donc l'equation de la tangente au point d'abscisse O est

6)Tracer les asymptotes,la tangente T et la courbe C

A faire par tes soins

7)Verifier que pr tout x de E,f(x)-8/3x=-8x3+28x²/3(x²-2x-3)
en dedire les coordonnees des pts communs a T et a (C)
Determiner les positions relatives de la tangente T et de la courbe (C)

on calcule f(x)-8/3x soit



si on appelle T(x) l'equation de la tangente au point d'abscisse O alors T(x)=8/3x pour trouver les coordonnées des points d'intersection entre C et T il suffit de resoudre f(x)=T(x) soit f(x)-T(x)=0 f(x)-8/3x=0 donc on a montrer que :


donc il faut resoudre:










on connait les abscisses des points d'intersections il ne reste plus qu'à trouver leurs ordonnées on remplace la valeur de x par exemple dans l'equation de T(x) .

pour x=0 y=0 , pour x=7/2 y=28/3

donc 2 points d'intersections de coordonnées (0,0) et (7/2,28/3)


pour etudier la position relative de C par rapport à T il faut etudier le signe de la difference d(x)=f(x)-8/3x soit

essaie de le faire en faisant un tableau de signe

pour la conclusion:
si d(x)>0 alors C est au dessus de T
si d(x)<0 alors T est au dessus de C


si tu n'y arrives pas faissigne

[hiller]

:we: merci beaucoup pour ton aide je ne sais pas comment tu fais pour que tout soit si simple!!!je me rends compte que j'ai pas mal de boulot pour une remise à niveau.Sur mon devoir j'ai trois exercice j'ai reussi le premier et il m'en reste encore un pourrais tu m'aider?

[hiller]

Voici l'enoncé:
Une entrprise qui fabrique des objets estime le cout total de production de x tonnes d'objets s'exprime,en fonction de x, par C(x)=x3-12x²+60x
Le cout total c(x) est exprimé en milliers d'euros.On notera 1keuro=1000euro
on designe par C la courbe representative de la fonction C dans un repere orthogonal
1cm pour 1tonnes et 1cm pour 20keuro en ordonnée
1)etudier les variations de la fonction C sur [0;-~[
2)le cout moyen de production est donné par Cm(x)+C(x)/x xsup à 0
quel est le cout moyen de fabrication
Soit A le point de C d'abscisse 6 et T la tangente a C en A
Determiner une equation de T
3)Etudier les variation sde la fonction Cm sur]0;+~[
4)on appelle cout marginal de x le cout de fabrication de la (x+1)e tonne.On le note Cma et on admet que:
Cma(x)+C'(x) ou C' est la fonction derivée de C
Etudier les variation de Cma sur [0;+~[
Determiner par le calcul l'abscisse beta du point d'interception K des courbes Cm et Cma
Que represente Cm(beta) pour la fonction Cm?