Besoin d'aide : Second Degré : Première S

par **bac2012s** » 16 Oct 2011, 21:14

bac2012s a écrit:Donc on trouve -2 et 1.5

Je te donne un indice donc

Ne lis pas la suite tant que tu n'as pas trouvé...

En combinant avec x² cela donne : x²=-2 et x²=1.5 donc on trouve

On sait que l'équation à pour solution -2 et 1.5. On en déduit que L'équation E aura pour solution la racine carré des solution du fait que X = x².
Mais l'équation doit être égale à 0 (il faudrait mettre une meilleure phrase je pense...)

En remplaçant x par
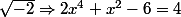
En remplaçant x par

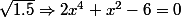
(0 = axe des abscisses)

-2 n'égalant pas 0, on l'exclu donc de la solution de léquation

1.5 est un nombre réel positif, on a alors pour solution de léquation :

Avec la TI89 :
solve(2x^4+x^2-6=0,x) ENTER

Par contre avec la TI83 c'est possible ?

----------------------------
PS : Pour me contacter : https://plus.google.com/i/JAwCkcvGqxc:eVNe51GK9Cw

il n'y a pas une meilleure façon de le réaliser, mes "phrases" sont correctes ?

par **MelleMeg** » 17 Oct 2011, 18:10

Oui tes phrases sont claires mais je demandais pour l'exercice 2 ^^'
Donc, j'ai commencé à résoudre la question de l'exercice 2 :
F(x) = 4x² - 5 / x² + x + 1
Donc il faut montrer que pour tout réel x, F(x) < 5 :
Donc on met au même dénominateur soit : 4x² - 5 / x² + x + 1 + - 5x² - 5x - 5 / x² + x + 1
Donc ce qui nous donne : - 1x² - 5x - 10 / x² + x + 1 < 0
On peut ensuite calculer le disriminant de ces 2 fonctions trinômes :
Discriminant de -1x² - 5x - 10 : (-5)² - 4 * (-1) * (-10) = -15 Donc comme Delta < 0 il n'y a pas de solutions réelles.
Discriminant de x² + x + 1 : 1² - 4 * 1 * 1 = - 3. Pas de solutions réelles

Pour F(x) > -6 :
Même dénominateur soit : 4x² - 5 / x² + x + 1 + - 6x² - 6x - 6 / x² + x + 1
Ce qui nous donne : - 2x² - 6x - 11 / x² + x + 1
On calcule ensuite les discriminants des 2 trinômes :
Discriminant de - 2x² - 6x - 11 : (-6)² - 4 * (-2) * (-11) = 36 - 88 = -52. Pas de solutions réelles.
Discriminant de x² + x + 1 : Déjà calculé en haut.

Et faut-il faire un tableau de signe pour chaque cas ? ( F(x) < 5 et F(x) > -6 )

par **Teacher** » 17 Oct 2011, 18:13

Tu as déjà travaillé sur les dérivées ?

par **MelleMeg** » 17 Oct 2011, 18:26

Nan pas encore =$

par **Teacher** » 17 Oct 2011, 18:42

C'est un peu illisible, pour le 2)
Montrer que F(x)<5 c'est prouver que:

Delta < 0 oui alors le trinôme est du signe de a "partout" a=-1 donc le trinôme est bien négatif sur R.
Alors l'inéquation est vraie et on a donc F(x)<5 sur R.

par **Teacher** » 17 Oct 2011, 18:47

Essaye de refaire la même chose pour F(x) > -6. ( tu t'es trompé !)

par **MelleMeg** » 17 Oct 2011, 19:15

Ok Merci de ta réponse :)
Mais on doit faire un tableau de signe avec =$
Donc il faut étudier le signe de -5x² -5x -5 , ensuite, celui de x² + x + 1 et pour terminer -5x² - 5X - 5 / x² + x = 1 C'est ça ? :x

par **MelleMeg** » 17 Oct 2011, 19:15

Je me suis trompé dans les calculs ?

par **Teacher** » 17 Oct 2011, 19:18

Où est le problème ? F(x)>-6 si et seulement si:

par **MelleMeg** » 17 Oct 2011, 19:36

Ok Donc ensuite il faut quand même faire le Delta ?

par **Teacher** » 17 Oct 2011, 19:39

Ensuite il faut donc prouver que:

Est-ce que c'est vraie pour tout x de R ?

par **MelleMeg** » 17 Oct 2011, 20:04

Beh je pense que Oui :x Après comment le démontrer j'ai du mal, on a pas trop travailler dessus =$
Mais je sais que notre prof nous a dit d'établir un tableau de signe :/

par **Teacher** » 17 Oct 2011, 20:24

Tu as travailler sur les trinômes ? Sur les tableaux de signe suivant le signe de delta ...
Ici tu cherches quand est ce que le terme de gauche est plus grand que 0 ....

par **MelleMeg** » 17 Oct 2011, 20:30

Oui, je l'ai fait ça j'ai calculé le delta un peu plus haut mais comme j'ai faux ... =$

par **Teacher** » 17 Oct 2011, 20:34

La solution est là !

Teacher a écrit:Ensuite il faut donc prouver que:

Est-ce que c'est vraie pour tout x de R ?

par **MelleMeg** » 17 Oct 2011, 20:35

Alors je l'ai recalculé pour F(x) > -6. Delta est égale à -4 donc pas de solutions réelles.
Par contre je comprends pas pourquoi mes calculs sont faux enfin pourquoi on ne fait pas apparaître x² + x + 1 :$ Bref, alors cette fonction est tout le temps croissante sur R.

par **Teacher** » 17 Oct 2011, 20:43

Tout le temps croissante ? pourquoi cette grosse bêtise ?

par **MelleMeg** » 17 Oct 2011, 20:54

Oops ^^' Dsl je suis pas très douée j'ai eu 5,5 au contrôle :'( Et le prof' explique bien mais trop vite donc pas le temps de suivre :'( Je suis perdu parce que là on est en train de faire un chapitre sur L'étude des fonctions et on revient sur le Second degré bref ... Je suis pommée ...
... Pas de solutions réelles donc la parabole est toujours au dessus l'axe des abcisses. Mais après pour déterminer d'où à où je bloque.

par **Teacher** » 17 Oct 2011, 21:05

Avec "ta" méthode cela donne:

par **MelleMeg** » 17 Oct 2011, 21:09

Mais cette méthode est juste ?

Besoin d'aide : Second Degré : Première S

Qui est en ligne