Salut,
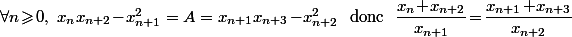
ce qui montre que le rationnel

est indépendant de

et vaut systématiquement

.
- Si

et

sont entiers, alors, du fait que
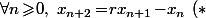)
, les

sont bien tous entiers.
- Réciproquement, si les

sont tous entiers, écrivons

(irréductible) et, pour tout

, posons

. La suite
_{n\geqslan 0})
est une suite d'entiers qui vérifie la relation
)
donc, pour tout

est entier ce qui signifie que

divise

. Comme

, l'entier

divise en fait tout les

. La suite
_{n\geqslant 0})
est donc de nouveau une suite d'entiers commençant par

et vérifiant
)
donc tous ses termes sont de nouveau divisibles par

. Etc . . .
Les termes de la suite
_{n\geqslan 0})
sont donc tous divisible par n'importe quelle puissance de

ce qui n'est possible que si

, c'est à dire

entier ou bien s'ils sont tous nuls. Or, le deuxième cas impliquerais que

ce qui est contraire à l'énoncé (

).

