Logique et calcul
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
clamat29
- Messages: 2
- Enregistré le: 18 Fév 2022, 15:39
-
 par clamat29 » 18 Fév 2022, 15:44
par clamat29 » 18 Fév 2022, 15:44
Bonjour, j'ai un exercice de maths à réaliser mais je n'y arrive pas. Pouvez vous m'aidez ?
Voici l'énoncé :
Soient a et b deux réels strictement positifs tels que √a/b+√b/a=√5. calculer|√a/b-√b/a|
( les racines sont sur le a et le b a chaque fois)
Merci à ceux qui prendront de leur temps pour m'aider

Modifié en dernier par
clamat29 le 18 Fév 2022, 20:58, modifié 1 fois.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 18 Fév 2022, 15:57
par GaBuZoMeu » 18 Fév 2022, 15:57
Bonjour,
Un bon réflexe est de regarder ce qui se passe quand on élève au carré.
PS. La prochaine fois, fais un effort pour mettre un titre plus informatif. Tout étudiant qui pose une question ici le fait parce qu'il a besoin d'aide !
-
mathelot
 par mathelot » 18 Fév 2022, 16:10
par mathelot » 18 Fév 2022, 16:10
clamat29 a écrit:Soient a et b deux réels strictement positifs tels que √a/b+√b/a=√5.
bonjour,

et

sont inverses l'un de l'autre.
Poser une équation du second degré.
-
catamat
- Habitué(e)
- Messages: 1364
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 18 Fév 2022, 18:34
par catamat » 18 Fév 2022, 18:34
Bonjour
On a deux nombres dont on connait la somme
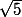
et le produit 1 (car comme l'a dit Mathelot, ils sont inverses l'un de l'autre). On peut donc calculer toute expression symétrique par rapport à ces deux nombres comme par exemple le carré de leur différence, etc...
-
mathelot
 par mathelot » 18 Fév 2022, 20:54
par mathelot » 18 Fév 2022, 20:54
question 1x,y réels , calculer
^2)
en fonction de
^2)
et de
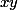
En déduire les valeurs possible de
 question 2
question 2a,b réels >0
On a
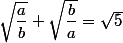
on pose
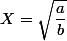
. Quelle équation du second degré vérifie

?
-
mathelot
 par mathelot » 19 Fév 2022, 10:57
par mathelot » 19 Fév 2022, 10:57
On pose
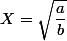
avec a,b>0
Il vient
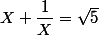
soit
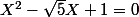
deux racines
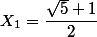
et
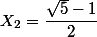
d'où
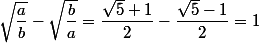
ou
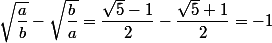
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 19 Fév 2022, 14:07
par GaBuZoMeu » 19 Fév 2022, 14:07
Comme je l'ai dit plus haut, un bon réflexe est d'élever au carré. Et ça donne la solution sans grand effort.
-
clamat29
- Messages: 2
- Enregistré le: 18 Fév 2022, 15:39
-
 par clamat29 » 19 Fév 2022, 16:06
par clamat29 » 19 Fév 2022, 16:06
Merci beaucoup à vous tous pour votre aide

-
mathelot
 par mathelot » 19 Fév 2022, 16:51
par mathelot » 19 Fév 2022, 16:51
GaBuZoMeu a écrit:Comme je l'ai dit plus haut, un bon réflexe est d'élever au carré. Et ça donne la solution sans grand effort.
bonjour GBZM,
j'avais mal lu l'énoncé. On fait l'hypothèse que les nombres

et

existent (donc pas besoin de calculer leurs valeurs) et de plus le résultat à démontrer est en valeur absolue.
donc
^2=\dfrac{a}{b}+\dfrac{b}{a}-2)
^2=\dfrac{a}{b}+\dfrac{b}{a}+2-4)
^2=\left( \sqrt{\dfrac{a}{b}}+\sqrt{\dfrac{b}{a} \right)^2-4=5-4=1)
d'où
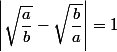
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités