Ideal

[LauraLe]

Bonjour,

Il y a un exercice qui me semble "simple" quand je lis l'énoncé mais j'ai l'impression ce que j'ai fait n'est pas correcte. Voici l'énoncé :

(un anneau commutatif et unitaire) des idéaux et un idéal premier tel que .
Vous montrerez que ou .

----------------------------------------------------------------------------------------------------------------------------------------

Par définition, est de la forme avec et
Or
Donc

Et après j'ai envie de dire que donc

ou Car P premier

Or et

Donc ou

[GaBuZoMeu]

Bonjour,

Tu as raison de douter : ce que tu as fait ne va pas.

D'abord, le produit des idéaux I et J n'est pas l'ensemble des produits xy avec x dans I et y dans J. C'est l'idéal engendré par ces produits.

Ensuite, ce que ton raisonnement montre, c'est que
pour tout x de I et tout y de J, (x appartient à P ou y appartient à P).
Mais ce que tu dois montrer c'est que
(pour tout x de I, x appartient à P) ou (pour tout y de J, y appartient à P)
ce qui n'est pas la même chose. Vois-tu la différence ?

[LauraLe]

Bonjour,

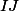
D'accord, en fait je pensais que était l'ensemble des sommes finies de termes de la forme.
C'est-à-dire le produit des idéaux de et est l'idéal engendré par =

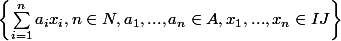
Oui je vois que ce n'est pas pareil. Par conséquent, je pense que je démarre mal...

Il faut donc que je parte de :

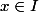
pour tout et montrer que
ou
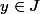
pour tout et montrer que

Si j'essaye de commencer:
I est un idéal de A donc par définition :
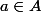
pour tout , pour tout ,

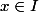
on sait que P est un idéal premier de A c'est à dire :
pour tout ou

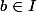
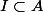
Or donc pour tout

D'après la définition de l'idéal premier on a :
Pour tout ou

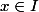
En faiit, je ne sais pas s'il faut commencer comme ceci mais j'ai l'intuition qu'il faut utiliser la définition d'un idéal premier (qui contient ce "ou") pour la question.

[GaBuZoMeu]

Indication : suppose que I n'est pas inclus dans P (s'il est inclus dans P, tu as gagné). Qu'as-tu alors à montrer ?

[LauraLe]

Vous voulez dire que je dois montrer par l'absurde que I est inclus dans P en montrant que I pas inclus dans P implique le faux ?

Si I n'est pas inclus dans P alors je dois montrer que J est inclus dans P je pense.

[GaBuZoMeu]

Vous voulez dire que je dois montrer par l'absurde que I est inclus dans P en montrant que I pas inclus dans P implique le faux ?

Non, ce n'est absolument pas ce que je veux dire.

Si I n'est pas inclus dans P alors je dois montrer que J est inclus dans P je pense.

Eh bien vas-y !

[LauraLe]

Si j'essaye :

Supposons que n'est pas inclus dans .

On a

Pour tout , pour tout ou

Oret n'est pas inclus dans , donc ne peut pas appartenir à .
Donc c'est à dire

Et après, il faut faire pareil avec cette fois-ci n'est pas inclus dans ?

[GaBuZoMeu]

Tu as quelques petits problèmes de logique, dirait-on.

1°) Bien préciser les quantificateurs. Dire que I n'est pas contenu dans P, c'est dire qu'il existe un élément a de I qui n'appartient pas à P

Dans ce que tu écris, tu donnes l'impression de penser qu'aucun élément de I n'appartenait à P

2°) Quand on montre que "si I n'est pas inclus dans P, alors J est inclus dans P", on montre que "I est inclus dans P ou J est inclus dans P".
L'assertion "Si non X, alors Y" est logiquement équivalente à l'assertion "X ou Y".

[LauraLe]

Effectivement oui !

D'accord si je comprends si j'arrive à montrer que si n'est pas inclus dans , alors est inclus dans alors j'aurai répondu à la question.

Si je reprends :
Supposons que n'est pas inclus dans
c'est-à-dire il existe tel que n'appartient pas à

On a

Définition d'un idéal premier:
Pour tout , pour tout ou

Or il existe un tel que ne peut pas appartenir à .

Donc c'est à dire

[GaBuZoMeu]

C'est en gros ça. Mais je rédigerai plutôt comme ça.

On suppose .
Supposons que n'est pas inclus dans . Alors il existe un tel que . Pour tout élément de , on a et donc ; puisque et premier et que , nécessairement . On a montré .
Par conséquent ou .

[LauraLe]

Oui c'est clair comme ça !

Je vous remercie !
Bonne soirée !

[GaBuZoMeu]

Avec plaisir.