Déjà répondu : tu as un minorant qui est fini !
Comment veux-tu que la borne inférieure ne le soit pas ?
Théorème de la limite monotone
23 messages
- Page 2 sur 2 - 1, 2
Re: Théorème de la limite monotone
par Kolis » 27 Aoû 2019, 19:27
Modifié en dernier par Kolis le 27 Aoû 2019, 19:34, modifié 2 fois.
Re: Théorème de la limite monotone
par Kolis » 27 Aoû 2019, 19:32
Mais bon sang !, ouvre les yeux !
Pour une fonction croissante, la limite à droite est une borne inférieure.
Tu as indiqué un minorant)
: donc la borne inférieure est finie.
Pour une fonction croissante, la limite à droite est une borne inférieure.
Tu as indiqué un minorant
Re: Théorème de la limite monotone
par mehdi-128 » 27 Aoû 2019, 20:15
J'ai enfin compris votre remarque. Merci pour votre aide.
Le problème est que dans mon livre, l'auteur n'a pas démontré le théorème de la limite monotone dans le cas de la limite en
. L'ayant fait, je viens de comprendre !
Étudions la limite en de 
.
1er cas :)
minoré.
Posons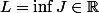
Soit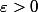
Par définition de la borne inférieure, il existe un 
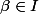tel que :  \leq L+\varepsilon)
On a par ailleurs \geq L)
Pour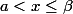
c'est-à-dire pour 
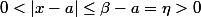on a par croissance de :
 \leq f(x) \leq f(\beta) \leq L+\varepsilon)
On a montré que-L| \leq \varepsilon)
Ainsi :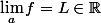
la limite est bien finie.
2ème cas : non minoré.
Alors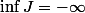
Soit
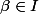un réel. Il existe tel que  \leq M)
. Ainsi on a pour 
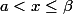:  \leq f(\beta) \leq M)
Soit par définition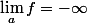
Le problème est que dans mon livre, l'auteur n'a pas démontré le théorème de la limite monotone dans le cas de la limite en
Étudions la limite en
1er cas :
Posons
Soit
On a par ailleurs
Pour
On a montré que
Ainsi :
2ème cas :
Alors
Soit
Soit par définition
23 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :