DM math
54 messages
- Page 3 sur 3 - 1, 2, 3
Re: DM math
Salut,
Je trouve plutôt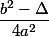
Je trouve plutôt
Modifié en dernier par laetidom le 13 Oct 2018, 13:18, modifié 1 fois.
Re: DM math
Bonjour
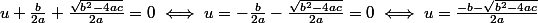
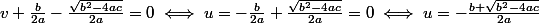
maintenant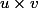
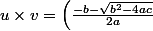 \times \left(\frac{-b + \sqrt{b^2 - 4ac}}{2a}\right))
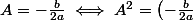^2)
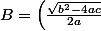 \iff B^2 = \left(\frac{\sqrt{b^2 - 4ac}}{2a}\right)^2)
^2 - \left(\frac{\sqrt{b^2 - 4ac}}{2a}\right)^2 <=> \frac{b^2}{4a^2} -\frac{b^2 - 4ac}{4a^2} <=>)
je peux éliminer les
ce qui me donne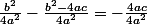
je simplifie le 4 du numérateur et le 4 du dénominateur
- ac/a^2
puis je simplifie le carré avec le a
et j'ai -a/c
c'est plus facile avec l'identité remarquable
maintenant
je peux éliminer les
ce qui me donne
je simplifie le 4 du numérateur et le 4 du dénominateur
- ac/a^2
puis je simplifie le carré avec le a
et j'ai -a/c
c'est plus facile avec l'identité remarquable
Re: DM math
Bonjour,
c'est presque bien mais quand tu arrives à
Tu devrais trouver c/a
c'est presque bien mais quand tu arrives à
attention aux erreurs de calcul.galereenpremièreS a écrit:\frac{b^2}{4a^2} -\frac{b^2 - 4ac}{4a^2}
Tu devrais trouver c/a
Re: DM math
Bonjour
pour la question1)
Montrer que les fonctions polynômes et
et  définies pour tout
définies pour tout 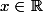
 = 2x^2 - 3x + 1)
et par = x^2 - \frac{3}{2} x + \frac{1}{2}) ont les mêmes racines.
ont les mêmes racines.
j'ai mis
 = 2x^2 - 3x + 1 =2 \left[x^2 - \frac{3}{2}x + \frac{1}{2}\right]<=> 2\times f_2(x))
Le calcul a montré que les 2 racines de c'est
c'est  et
et 
je fais la démonstration pour une racine :
^2 - 3(1) +1 = 0 <=> f_1(1) = 0)
et = 0) cela entraine
cela entraine  = 0 <=> 2 * f_2(1) = 0 <=> f_2(1) = 0)
j'en déduis que) a même racine que
a même racine que 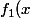)
pour la question1)
Montrer que les fonctions polynômes
et par
j'ai mis
Le calcul a montré que les 2 racines de
je fais la démonstration pour une racine :
et
j'en déduis que
Re: DM math
Bonjour
oui, c'est vrai
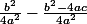
ce qui signifie ( avec la parenthèse )
}{4a^2} = \frac{b^2}{4a^2} +\frac{-b^2 + 4ac}{4a^2})
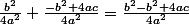
b au carré moins b au carré -> ça disparait
j'écris alors :
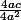
le 4 au numérateur et le 4 au dénominateur s'éliminent
il me reste alors :
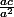
le carré et le a du numérateur
ainsi :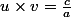
-
oui, c'est vrai
ce qui signifie ( avec la parenthèse )
b au carré moins b au carré -> ça disparait
j'écris alors :
le 4 au numérateur et le 4 au dénominateur s'éliminent
il me reste alors :
le carré et le a du numérateur
ainsi :
-
Re: DM math
Bonjour
pour la question1)
Montrer que les fonctions polynômes et
et  définies pour tout
définies pour tout 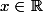
 = 2x^2 - 3x + 1)
et par = x^2 - \frac{3}{2} x + \frac{1}{2}) ont les mêmes racines.
ont les mêmes racines.
j'ai mis
 = 2x^2 - 3x + 1 =2 \left[x^2 - \frac{3}{2}x + \frac{1}{2}\right]<=> 2\times f_2(x))
Le calcul a montré que les 2 racines de c'est
c'est  et
et 
je fais la démonstration pour une racine :
^2 - 3(1) +1 = 0 <=> f_1(1) = 0)
et = 0) cela entraine
cela entraine  = 0 <=> 2 * f_2(1) = 0 <=> f_2(1) = 0)
j'en déduis que) a même racine que
a même racine que 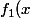)
-
pour la question1)
Montrer que les fonctions polynômes
et par
j'ai mis
Le calcul a montré que les 2 racines de
je fais la démonstration pour une racine :
et
j'en déduis que
-
54 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
