[ TS Spé Math / Math Obligatoire ] PPCM & Fonction Ln

[Ailin]

Bonjour à tous,

Je viens à vous pour vous présenter deux problèmes qui me sont posés, en espérant que vous pourrez m'orienter.

• Le premier est une partie d'un DM de Spécialité.

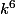
Il s'agit de trouver la plus petite valeur de k pour laquelle est un multiple de 2008 [ En utilisant la décomposition de 2008 en facteurs premiers, soit ]

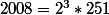
• Le second est un exercice de Mathématiques obligatoires

Il s'agit ici de soucis de rédaction, et je me demandais si vous pouviez me venir en aide. Le but est d'étudier une fonction
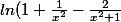
On fait une étude auxiliaire d'une fonction G(x) que l'on prouvera ensuite être la dérivée de f(x). G(x)= sur ]0,[
Donc, on me demande d'étudier la limite de x(f(x)) lorsque x tend vers , puis d'en désuire que f(x) tend vers 0 lorsque x tend vers +, et là je suis un peu perdue oÔ. Je n'arrive pas à me sortir de la forme indéterminée, pour commencer. J'aurai eu tendance à transformer la fonction Ln en ln(x²+1)-2ln(x), mais on me demande de le faire plus tard, ce qui semble étonnant ...

Je réfléchis encore au reste, et si je ne m'en sors pas, peut-être que les aides concernant ceci pourront m'aider.

Merci par avance !

[dudumath]

251 est premier il me semble donc k doit contenir 251 dans sa décomposition en facteurs premiers

De plus, k est pair puisque k^6 l'est:on en déduit:

k=2*251
et par construction, c'est la plus petite

[Nightmare]

Salut !

1) Il suffit d'examiner la décomposition en facteur premier de k. Exemple : Celle-ci contient forcément 2. Comme k^6 doit être divisible par 2^3, la puissance minimal qu'on peut prendre pour k est 2^1. On sait aussi que k^6 doit contenir 251 dans sa décomposition en facteur premier donc forcément que k aussi, et au minimum à la puissance 1.

Finalement, convient et est le plus petit.

[Ailin]

Alors, Ahem.

1) Je ne suis pas bien sûre, Nightmare, d'avoir saisi pourquoi la décomposition en facteurs premiers de k devait contenir 2 - Et à fortiori, le reste encore moins. Je suis désolée de tant d'incompréhension. Il s'agit d'un cours auquel je n'ai pas assisté, et je suis un peu en marge ...

2) Jéjouille > Croissance comparée ? Ahem, là, par contre, je n'ai jamais vu oÔ
Cela dit, tu dois être dans le juste, parce qu'ils proposent de poser h=1/x² , dans l'énoncé ...